Các câu hỏi tương tự
Viết phương trình đường thẳng d đi qua tâm mặt cầu
S
:
x
2
+
y
2
+
z
2
−
4
x
−
6
y
+
6
z
+
17
0
Và vuông góc với mặt phẳng
P
:
x
−
2
y
+
2
z
+...
Đọc tiếp
Viết phương trình đường thẳng d đi qua tâm mặt cầu S : x 2 + y 2 + z 2 − 4 x − 6 y + 6 z + 17 = 0
Và vuông góc với mặt phẳng P : x − 2 y + 2 z + 1 = 0.
A. x = 5 + 4 t y = 3 + 3 t z = − 2 + 4 t .
B. x = 1 + t y = 3 + 7 t z = − 2 + 4 t .
C. x = 2 + t y = − 3 − 2 t z = − 3 + 2 t .
D. x = 1 + t y = 3 − 7 t z = − 3 + 2 t .
Viết phương trình đường thẳng d đi qua tâm mặt cầu
S
:
x
2
+
y
2
+
z
2
-
4
x
+
6
y
+
6
z
+
17
0
. Và vuông góc với mặt phẳng
P
:
x
-
2
y
+
2...
Đọc tiếp
Viết phương trình đường thẳng d đi qua tâm mặt cầu S : x 2 + y 2 + z 2 - 4 x + 6 y + 6 z + 17 = 0 . Và vuông góc với mặt phẳng P : x - 2 y + 2 z + 1 = 0 .
A. x = 5 + 4 t y = 3 + 3 t z = - 2 + 4 t
B. x = 1 + t y = 3 + 7 t z = - 2 + 4 t
C. x = 2 + t y = - 3 - 2 t z = - 3 + 2 t
D. x = 1 + t y = 3 - 7 t z = - 3 + 2 t
Cho mặt phẳng
P
:
x
-
2
y
+
2
z
+
1
0
cắt mặt cầu (S) có phương trình
S
:
x
2
+
y
2
+
z
2
-
4
x
+
6
y
+
6
z
+
17...
Đọc tiếp
Cho mặt phẳng P : x - 2 y + 2 z + 1 = 0 cắt mặt cầu (S) có phương trình S : x 2 + y 2 + z 2 - 4 x + 6 y + 6 z + 17 = 0 theo đường tròn. Tính chu vi của đường tròn đó.
A. 4 π
B. π
C. 6 π
D. 8 π
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với (S):
x
2
+
y
2
+
z
2
-
2
z
-
4
y
-
6
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với (S): x 2 + y 2 + z 2 - 2 z - 4 y - 6 z - 2 = 0 và song song với (α): 4x + 3y - 12z+10 = 0
A. 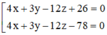
B. 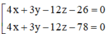
C. 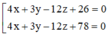
D. 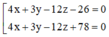
Trong không gian Oxyz cho mặt cầu (S)
x
2
+
y
2
+
z
2
-
2
x
-
4
y
-
6
z
-
2
0
và mặt phẳng
α
4
x
+
3
y
-...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu (S) x 2 + y 2 + z 2 - 2 x - 4 y - 6 z - 2 = 0 và mặt phẳng α 4 x + 3 y - 12 z + 10 = 0 . Lập phương trình mặt phẳng β thỏa mãn đồng thời các điều kiện: Tiếp xúc với (S), song song với α và cắt trục Oz ở điểm có cao độ dương
A. 4 x + 3 y - 12 z - 78 = 0
B. 4 x + 3 y - 12 z - 26 = 0
C. 4 x + 3 y - 12 z + 78 = 0
D. 4 x + 3 y - 12 z + 26 = 0
Cho mặt cầu có phương trình
x
2
+
y
2
+
z
2
-
4
x
-
2
y
+
2
z
+
5
0
và mặt phẳng
P
:
3
x
-
2
y
+
6
z
+
m...
Đọc tiếp
Cho mặt cầu có phương trình x 2 + y 2 + z 2 - 4 x - 2 y + 2 z + 5 = 0 và mặt phẳng P : 3 x - 2 y + 6 z + m = 0 . S và P giao nhau khi
A. 2 ≤ m ≤ 3
B. m > 2 hoặc m < 2
C. - 5 ≤ m ≤ 9
D. m > 9 hoặc m < - 5
Cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
−
4
x
−
2
y
+
2
z
+
5
0
và mặt phẳng
P
:
3
x
−
2
y
+
6
z
+
m
0
. (S) và (P) giao nha...
Đọc tiếp
Cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 − 4 x − 2 y + 2 z + 5 = 0 và mặt phẳng P : 3 x − 2 y + 6 z + m = 0 . (S) và (P) giao nhau khi
A. m > 3 hoặc m < 2
B. m > 9 hoặc m < -5
C. − 5 ≤ m ≤ 9
D. 2 ≤ m ≤ 3
Cho mặt phẳng
α
:
4
x
+
y
+
2
z
+
1
0
và
β
:
2
x
-
2
y
+
z
+
3
0
. Viết phương trình tham số của đường thẳng d là giao của (α) và (β). A.
x...
Đọc tiếp
Cho mặt phẳng α : 4 x + y + 2 z + 1 = 0 và β : 2 x - 2 y + z + 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của (α) và (β).
A. x = t y = 1 - t z = - 1 - 2 t
B. x = t y = 1 z = - 1 - 2 t
C. x = - t y = 1 z = - 1 - 2 t
D. x = - t y = 1 + t z = - 1 - 2 t
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
4
x
-
2
y
+
4
z
0
và mặt phẳng
(
P
)
:
x
+
2
y
-
2
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 4 x - 2 y + 4 z = 0 và mặt phẳng ( P ) : x + 2 y - 2 z + 1 = 0 . Gọi (Q) là mặt phẳng song song với (P) và tiếp xúc với mặt cầu (S). Phương trình mặt phẳng (Q) là
A. ( Q ) : x + 2 y - 2 z - 17 = 0
B. ( Q ) : x + 2 y - 2 z - 35 = 0
C. ( Q ) : x + 2 y - 2 z + 1 = 0
D. ( Q ) : 2 x + 2 y - 2 z + 19 = 0
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn có phương trình
x
2
+
y
2
–
4
x
-
2
y
–
8
0
. Đỉnh A thuộc tia Oy, đường cao kẻ từ đỉnh C thuộc đường thẳng x + 5y 0. Tìm tọa độ đỉnh B của tam giác ABC. A. B (-1;-1) B. B (0;4...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn có phương trình x 2 + y 2 – 4 x - 2 y – 8 = 0 . Đỉnh A thuộc tia Oy, đường cao kẻ từ đỉnh C thuộc đường thẳng x + 5y = 0. Tìm tọa độ đỉnh B của tam giác ABC.
A. B (-1;-1)
B. B (0;4)
C. B (5;-1)
D. B (1;9)


