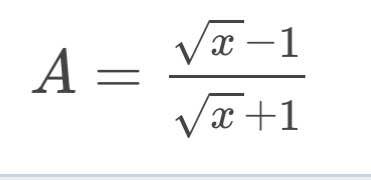\(A=\dfrac{x}{x+3}=1-\dfrac{3}{x+3}\in Z\)
\(\Rightarrow\left(x+3\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow x\in\left\{-6;-4;-2;0\right\}\)
\(A=\dfrac{x}{x+3}=1-\dfrac{3}{x+3}\in Z\)
\(\Rightarrow\left(x+3\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
\(\Rightarrow x\in\left\{-6;-4;-2;0\right\}\)
Bài 10. Cho 3 số dương x,y,z thỏa mãn: (√(xy/z)+√(xz/y)+√(yz/x)) = 3
Tìm GTNN của: P = (√x+√y+√z) + (2016/(√x+√y)) + (2016/√z)
a) Tìm ĐKXĐ và rút gọn M
b) Tìm x thuộc Z để M thuộc Z. Tìm giá trị nguyên đó
c) Tìm x thỏa mãn M<0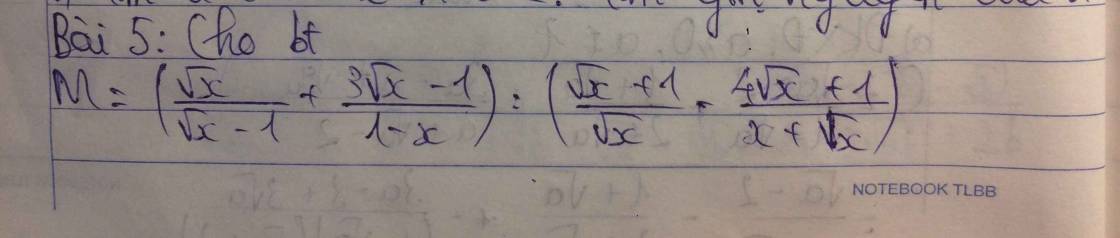
A=(x/x+3 - 2/x-3 + x^2-1/9-x^2):(2- x+5/3+x)
a;rút gọn biểu thức A
b;tìm A biết |x|=1
c;tìm x biết a=1/2
d; tìm các giá trị thuộc z để a thuộc giá trị nguyên
Tìm x thuộc Z để biểu thức có giá trị nguyên: A=\(\dfrac{2\sqrt{x}+3}{3\sqrt{x}-1}\)
Cho \(A=\frac{\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}}{\sqrt{1-\frac{2}{x}+\frac{1}{x^2}}}\)
a) Rút gọn A
b) Tìm x thuộc Z , x>2 để A nguyên
2,2. Cho biểu thức A = \(\frac{x+8\sqrt{x}+15}{x+\sqrt{x}-6}\)
Tìm x thuộc Z để biểu thức A nhận giá trị nguyên
Bài 1:
Cho E = \(\frac{1}{x+\sqrt{x}}\)
Tìm x thuộc Z để E có giá trị nguyên.
Bài 2:
Cho F = \(\frac{3}{x+\sqrt{x}+1}\)
Tìm x thuộc Z để F có giá trị nguyên.
Cho A= 3√x / √x - 3 với x >0, x khác 9. Tìm x thuộc Z để P thuộc Z
Tìm x thuộc Z để 2/A nhận giá trị nguyên dương lớn nhất