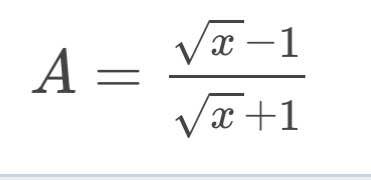Question

Tìm x thuộc Z để 2/A nhận giá trị nguyên dương lớn nhất

Answer 1

Lời giải:

Để $\frac{2}{A}$ dương thì $A$ dương

$\Leftrightarrow \sqrt{x}>1 \Leftrightarrow x>1$
\(\frac{2}{A}=\frac{2(\sqrt{x}+1)}{\sqrt{x}-1}=\frac{2(\sqrt{x}-1)+4}{\sqrt{x}-1}=2+\frac{4}{\sqrt{x}-1}\)

Để $A$ nhận giá trị nguyên dương lớn nhất thì $\sqrt{x}-1$ phải nhận giá trị nguyên dương nhỏ nhất.

Với $x>1$ thì $\sqrt{x}-1$ nguyên dương nhỏ nhất bằng $1$

$\Lefrightarrow \sqrt{x}=2$

$\Leftrightarrow x=4$

Vậy $x=4$ thì $\frac{2}{A}$ nhận giá trị nguyên dương lớn nhất.