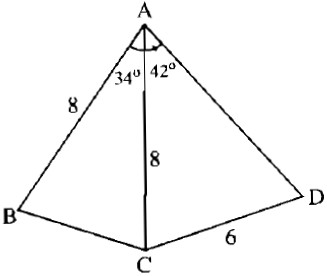
Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(cos35=\dfrac{8^2+8^2-BC^2}{2\cdot8\cdot8}\)
=>\(128-BC^2=2\cdot64\cdot cos35=128\cdot cos35\)
=>\(BC=\sqrt{128-128\cdot cos35}\simeq4,81\left(cm\right)\)
Xét ΔADC có \(\dfrac{CD}{sinCAD}=\dfrac{AC}{sinADC}\)
=>\(\dfrac{8}{sinADC}=\dfrac{6}{sin43}\)
=>\(sinADC=8\cdot\dfrac{sin43}{6}\simeq0,91\)
=>\(\widehat{ADC}\simeq65^0\)