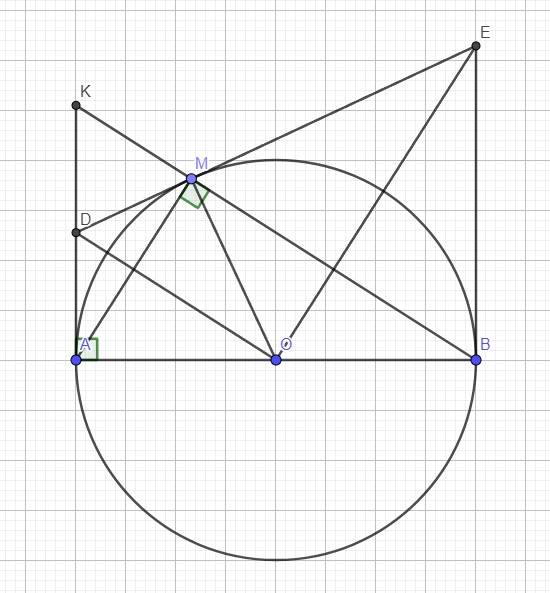
a.
Do AB là đường kính \(\Rightarrow\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{AMB}=90^0\Rightarrow\Delta AMB\) vuông tại M
b.
\(\widehat{AMK}=180^0-\widehat{AMB}=90^0\Rightarrow\Delta AMK\) vuông tại M
\(\Rightarrow MD\) là trung tuyến ứng với cạnh huyền
\(\Rightarrow MD=AD\)
Xét hai tam giác OAD và OMD có: \(\left\{{}\begin{matrix}OA=OM=R\\AD=MD\left(cmt\right)\\OD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAD=\Delta OMD\left(c.c.c\right)\)
\(\Rightarrow\widehat{OMD}=\widehat{OAD}=90^0\)
\(\Rightarrow DM\) là tiếp tuyến của (O).
c.
E là giao điểm 2 tiếp tuyến tại B và M \(\Rightarrow EM=EB\)
Mà \(OM=OB=R\Rightarrow OE\) là trung trực BM
\(\Rightarrow OE\) đồng thời là phân giác \(\widehat{BOM}\) hay \(\widehat{MOE}=\dfrac{1}{2}\widehat{BOM}\)
Tương tự ta có OD là phân giác \(\widehat{AOM}\Rightarrow\widehat{DOM}=\dfrac{1}{2}\widehat{AOM}\)
\(\Rightarrow\widehat{MOE}+\widehat{DOM}=\dfrac{1}{2}\left(\widehat{BOM}+\widehat{AOM}\right)\)
\(\Rightarrow\widehat{DOE}=\dfrac{1}{2}.180^0=90^0\)
Hay tam giác DOE vuông tại O
Áp dụng hệ thức lượng với đường cao OM:
\(DM.ME=OM^2\Leftrightarrow AD.BE=R^2\)