Các câu hỏi tương tự
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
v
ớ
i
a
,
b
,
c
,
d
∈
ℝ
,
a...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( v ớ i a , b , c , d ∈ ℝ , a > 0 ) . Biết đồ thị hàm số y=f(x) này có điểm cực đại A (0;1) và điểm cực tiểu B(2;-3). Hỏi tập nghiệm của phương trình f 3 ( x ) + f ( x ) - 2 f ( x ) 3 = 0 có bao nhiêu phần tử?
A. 2019
B. 2018
C. 9
D. 8
Cho F'(x) = f(x), C là hằng số dương tùy ý.
Khi đó 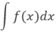 bằng:
bằng:
A. F(x) + C B. F(x) - C
C. F(x) + lnC D. F(x + C)
Cho F'(x) = f(x), C là hằng số dương tùy ý.
Khi đó ∫ f(x)dx bằng:
A. F(x) + C B. F(x) - C
C. F(x) + lnC D. F(x + C)
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số y f(x) liên tục trên đoạn [a;b] và f(x)0 Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và 2 đường thẳng xa; xb Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và f(x)>0 Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và 2 đường thẳng x=a; x=b Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
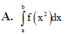
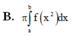
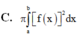
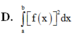
Gọi VV là thể tích vật thể tròn CC xoay được tạo thành khi quay miền D được giới hạn bởi các đường yfleft(xright);y0;xa;xbyf(x);y0;xa;xb quanh trục OxOx. Khẳng định nào dưới đây đúng?Vint_a^bf^2left(xright)text{d}xV∫abf2(x)dx.Vpiint_a^bf^2left(xright)text{d}xVπ∫abf2(x)dx.Vpi^2int_a^bfleft(xright)text{d}x.Vπ2∫abf(x)dx.Vpiint_a^bfleft(xright)text{d}xVπ∫abf(x)dx.
Đọc tiếp
Gọi VV là thể tích vật thể tròn CC xoay được tạo thành khi quay miền D được giới hạn bởi các đường y=f\left(x\right);y=0;x=a;x=by=f(x);y=0;x=a;x=b quanh trục OxOx. Khẳng định nào dưới đây đúng?
V=\int_a^bf^2\left(x\right)\text{d}xV=∫abf2(x)dx.
V=\pi\int_a^bf^2\left(x\right)\text{d}xV=π∫abf2(x)dx.
V=\pi^2\int_a^bf\left(x\right)\text{d}x.V=π2∫abf(x)dx.
V=\pi\int_a^bf\left(x\right)\text{d}xV=π∫abf(x)dx.
hàm số
f
(
x
)
ln
1
-
1
x
2
. Biết rằng
f
(
2
)
+
F
(
3
)
+
.
.
.
+
f
(
2018
)
ln
a
-
ln
b...
Đọc tiếp
hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968
Cho
F
log
a
1
x
4
.
log
1
b
2
c
.
log
1
a
b
.
log
c
1
a
3...
Đọc tiếp
Cho F = log a 1 x 4 . log 1 b 2 c . log 1 a b . log c 1 a 3 Đẳng thức nào dưới đây với ∀ a , b , c , d , x thỏa mãn: 0<a<b<c<d<x<1
![]()
![]()
![]()
![]()
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn
f
(
x
)
.
f
(
a
-
x
)
1...
Đọc tiếp
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn f ( x ) . f ( a - x ) = 1 f ( x ) > 0 ; ∀ x ∈ [ 0 ; a ] và ∫ 0 a d x 1 + f ( x ) = b a c , trong đó b, c là hai số nguyên dương và b/c là phân số tối giản. Khi đó b+c có giá trị thuộc khoảng nào dưới đây?
A. (11;22)
B. (0;9)
C. (7;21)
D. (2017;2020)
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1


