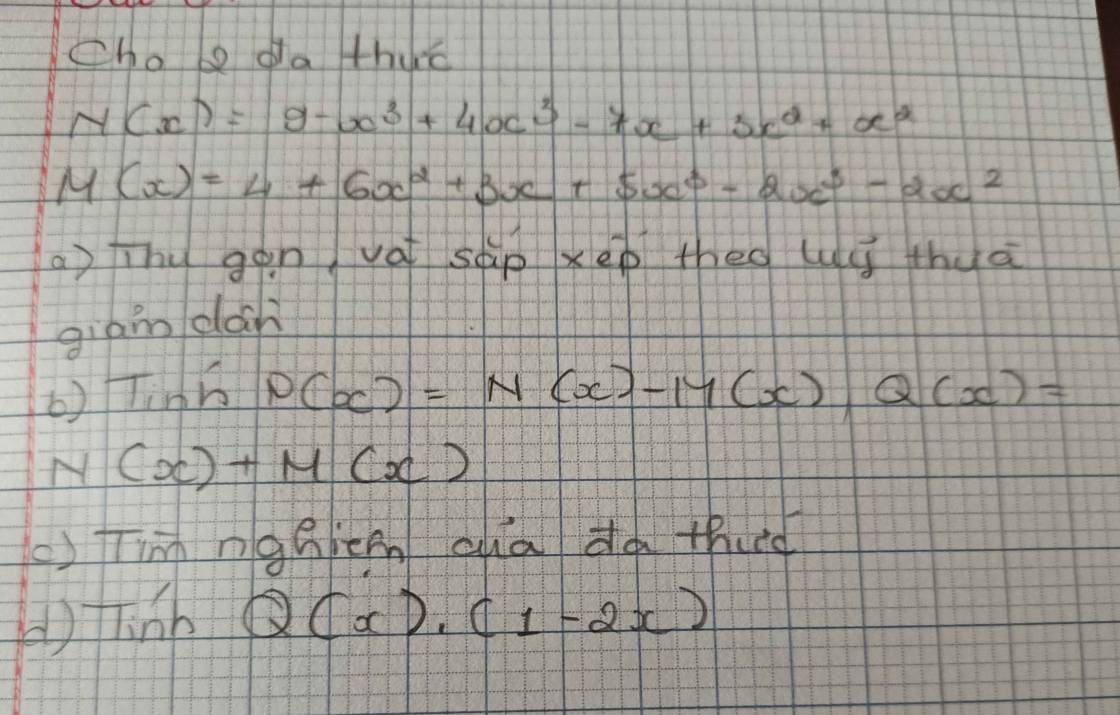a: Xét ΔOAM và ΔOBM có
OA=OB
AM=BM
OM chung
Do đó: ΔOAM=ΔOBM
b: Xét ΔOBH và ΔOAH có
OB=OA
\(\widehat{BOH}=\widehat{AOH}\)
OH chung
Do đó: ΔOBH=ΔOAH
Suy ra: HA=HB
c: Xét ΔOKE có
OA/OE=OB/OK
=>OA/OB=OE/OK=1
=>OE=OK
Ta có: ΔOEK cân tại O
mà OH là đường cao
nên OH là đường trung trực
Tacos
AB//EK
Mà AM=MB => M là trung điểm của EK
Ta lại có O,M,H thẳng hàng
=>H là trung điểm của EK
=>OH là đg trung trực của EK
a: Xét ΔOAM và ΔOBM có
OA=OB
AM=BM
OM chung
Do đó: ΔOAM=ΔOBM
b: Xét ΔOBH và ΔOAH có
OB=OA
Vì AB=AC
⇒ Tam giác OAB cân tại O
⇒ OM là đường trung tuyến đồng thời là đường cao
⇒ OM ⊥ AB
⇒ ^A=^B
Vì EK//AB
⇒ \(\left\{{}\begin{matrix}\text{^}A=\text{^}E\\\text{^}B=\text{^}K\end{matrix}\right.\) mà ^A=^B
⇒ \(\text{^}E=\text{^}K\)
⇒ Tam giác OEK cân tại O
⇒ \(HE=HK\)(1)
⇒ H là trung điểm EK
Vì O;M;H thẳng hàng mà OM⊥AB
⇒ OM⊥EK(2)
Từ (1) và (2)
⇒ OH là đường trung trực của EK
C2 )
Taco OB=OA
=> △OAB cân
AB //EK
=>△OEK cân
mà AM=MB
=> HE=HK
=> OH là đg trung trựccua EK