câu 1: rút ngọn biểu thức sau
\(A=\left(2\sqrt{3}+4\sqrt{27}-\sqrt{108}\right)\div2\sqrt{3}\)
\(B=\sqrt{9+4\sqrt{5}}-2\left(\sqrt{5}+1\right)\)
câu 2:
trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d1):y=x+2, (d2) : y=-x +4 và (d3) : y=mx+m. (m là tham số thực ).
a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ Oxy.
b) xác định các giá trị của hàm số m để đường thẳng (d3) đi qua giao điểm của (d1) và (d2).
câu 3:
Anh Hoàng thiết kế một ngôi nhà với phần mái có dạng hình tam giác cân ABC. Biết rằng góc tạo bởi phần mái và mặt phẳng nằm ngang là 28°, chiều dài mỗi bên mái là 3,8 m (minh họa như hình bên dưới). Tính khoảng cách giữa hai điểm B, C.
Câu 4. Cho nửa đường tròn tâm O, đường kính AB. Lấy điểm C thuộc nửa đường tròn (C khác A, khác B) sao cho CA <CB. Và OM vuông góc với AC, ON vuông góc với BC (M thuộc AC, N thuộc BC).
a) Chứng minh tứ giác OMCN là hình chữ nhật.
b) Tiếp tuyến tại A của nửa đường tròn tâm O cắt BC tại E, vẽ CH vuông góc với AB (H thuộc AB). Chứng minh: EC.CB = AH.AB.
c) Tiếp tuyến tại B của nửa đường tròn tâm O cắt ON tại F, OM cắt AE tại I. Chứng mình IF là tiếp tuyến của nửa đường tròn tâm O.
Câu 1:
\(A=\left(2\sqrt{3}+4\cdot\sqrt{27}-\sqrt{108}\right):2\sqrt{3}\)
\(=\dfrac{\left(2\sqrt{3}+4\cdot3\sqrt{3}-6\sqrt{3}\right)}{2\sqrt{3}}\)
\(=\dfrac{2\sqrt{3}+12\sqrt{3}-6\sqrt{3}}{2\sqrt{3}}=\dfrac{8\sqrt{3}}{2\sqrt{3}}=4\)
\(B=\sqrt{9+4\sqrt{5}}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{5+2\cdot\sqrt{5}\cdot2+4}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-2\left(\sqrt{5}+1\right)\)
\(=\sqrt{5}+2-2\sqrt{5}-2=-\sqrt{5}\)
Câu 2:
a: 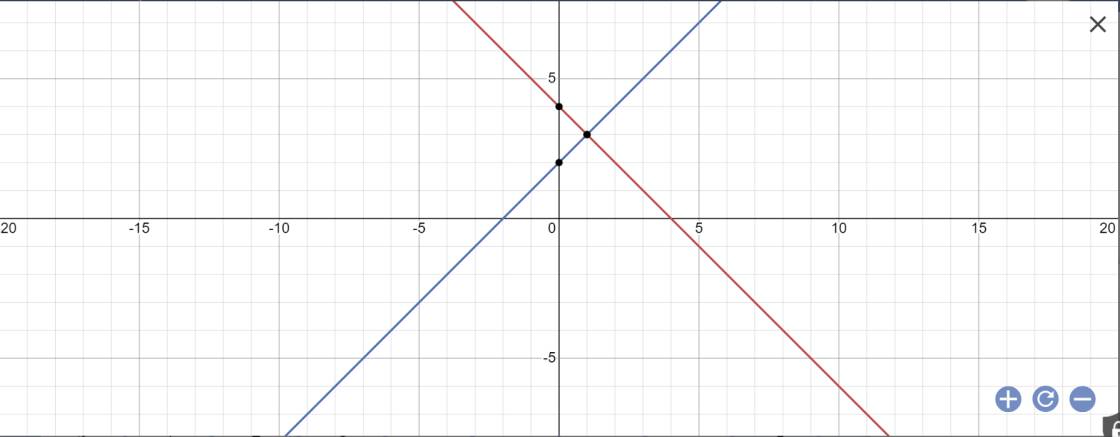
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(m\cdot1+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)
Câu 4:
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Xét tứ giác CMON có \(\widehat{CMO}=\widehat{CNO}=\widehat{MCN}=90^0\)
=>CMON là hình chữ nhật
b: Ta có: ΔCAB vuông tại C
=>CA\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔAEB vuông tại A có AC là đường cao
nên \(EC\cdot CB=AC^2\left(1\right)\)
Xét ΔCAB vuông tại C có CH là đường cao
nên \(AH\cdot AB=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(EC\cdot CB=AH\cdot AB\)
c: Ta có: ΔOAC cân tại O
mà OM là đường cao
nên OM là phân giác của góc AOC
Xét ΔOAI và ΔOCI có
OA=OC
\(\widehat{AOI}=\widehat{COI}\)
OI chung
Do đó: ΔOAI=ΔOCI
=>\(\widehat{OAI}=\widehat{OCI}=90^0\)
Ta có: ΔOBC cân tại O
mà ON là đường cao
nên ON là phân giác của góc COB
Xét ΔOBF và ΔOCF có
OB=OC
\(\widehat{BOF}=\widehat{COF}\)
OF chung
Do đó: ΔOBF=ΔOCF
=>\(\widehat{OBF}=\widehat{OCF}=90^0\)
Ta có: \(\widehat{ICF}=\widehat{ICO}+\widehat{FCO}\)
\(=90^0+90^0=180^0\)
=>I,C,F thẳng hàng
=>OC\(\perp\)IF tại C
Xét (O) có
OC là bán kính
IF\(\perp\)OC tại O
Do đó: IF là tiếp tuyến của (O)

