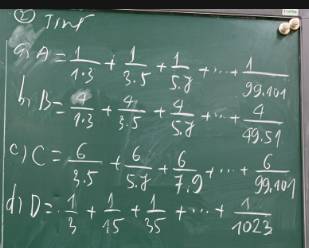a/\(A=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{99.101}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{101}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{100}{101}\)
\(=\dfrac{50}{101}\)
b/\(B=\dfrac{4}{1.3}+\dfrac{4}{3.5}+\dfrac{4}{5.7}...+\dfrac{4}{49.51}\)
\(=2\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{49.51}\right)\)
\(=2\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=2\left(1-\dfrac{1}{51}\right)\)
\(=2\cdot\dfrac{50}{51}\)
\(=\dfrac{100}{51}\)
c/\(C=\dfrac{6}{3.5}+\dfrac{6}{5.7}+\dfrac{6}{7.9}+...+\dfrac{6}{99.101}\)
\(=3\left(\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+...+\dfrac{2}{99.101}\right)\)
\(=3\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=3\left(\dfrac{1}{3}-\dfrac{1}{101}\right)\)
\(=3\cdot\dfrac{98}{303}\)
\(=\dfrac{98}{101}\)
d/\(D=\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{1023}\)
\(=\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{31.33}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{31.33}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{31}-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{33}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{32}{33}\)
\(=\dfrac{16}{33}\)
#TiendatzZz
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
a)(-0,25).4/17.(-3 5/21).(-7/12)
b) (-2/5).4/15+(-3/10).4/15
c)21-3 3/4:(3/8-1/6)
d) (-3/4+2/5):3/7+(3/5+-1/4):3/7
GIÚP MÌNH VỚI Ạ. MÌNH CẦN GẤP VÀO SÁNG NAY. CẢM ƯN NỌI NGƯỜI NHÌU!
CÔ NGUYỄN THỊ THƯƠNG HOÀI GIÚP EM VỚI Ạ
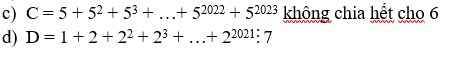
giúp em với ạ em cảm ơn em đang cần gấp ạ
Mọi người giúp em vơi em đang cần gấp ạ . Ai đúng và nhanh em tick ạ , em cảm ơn . Giúp em bài 5,6,7 ạ .

 Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.
Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.
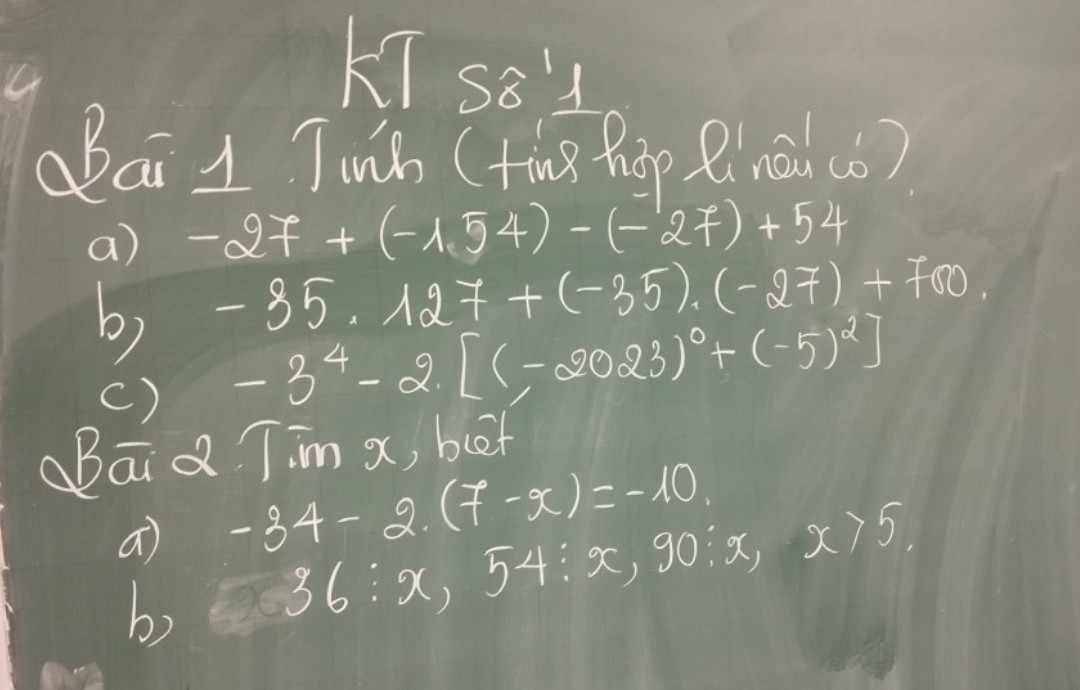 giúp em với ạ em đang cần gấp em cảm ơn ạ 😘😘
giúp em với ạ em đang cần gấp em cảm ơn ạ 😘😘

bài này khó quá ạ, có ai giúp mình đc khum, cảm ưn nhìu
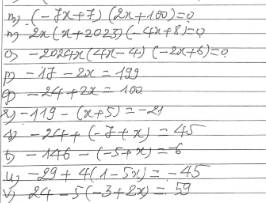
cần giúp gấp vs ạ, em cảm ơn
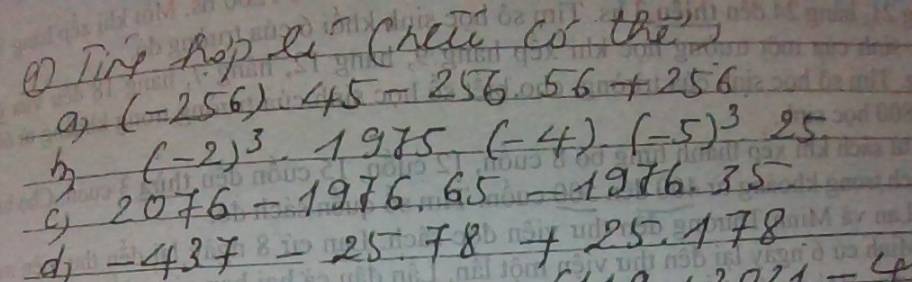 cần giúp gấp vs ạ, em cảm ơn nhìu
cần giúp gấp vs ạ, em cảm ơn nhìu

cần giúp gấp vs ạ , em cảm ơn nhìu