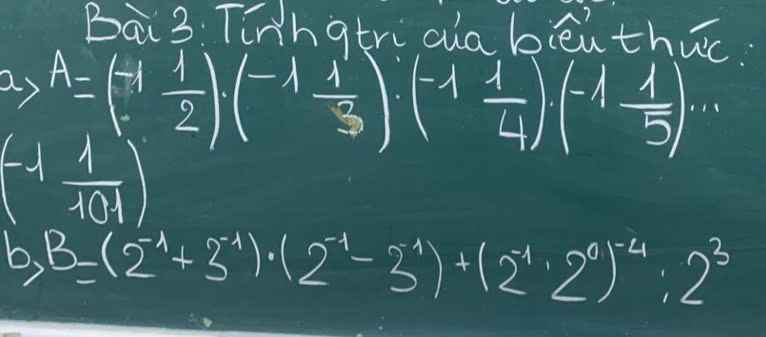a: \(A=\left(-1\dfrac{1}{2}\right)\cdot\left(-1\dfrac{1}{3}\right)\cdot...\cdot\left(-1\dfrac{1}{101}\right)\)
\(=-\dfrac{3}{2}\cdot\dfrac{-4}{3}\cdot...\cdot\dfrac{-102}{101}\)
\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{102}{101}=\dfrac{102}{2}=51\)
b: \(B=\left(2^{-1}+3^{-1}\right)\left(2^{-1}-3^{-1}\right)+\left(2^{-1}\cdot2^0\right)^{-4}:2^3\)
\(=\left(\dfrac{1}{2}+\dfrac{1}{3}\right)\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{2}\cdot1\right)^{-4}:8\)
\(=\dfrac{5}{6}\cdot\dfrac{1}{6}+16:8=\dfrac{5}{36}+2=\dfrac{77}{36}\)