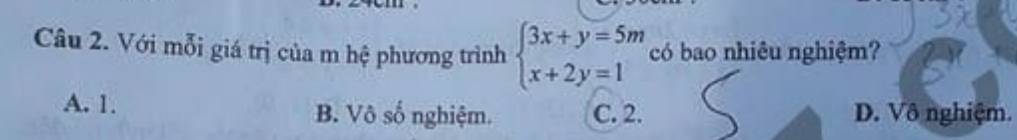ĐKXĐ: \(2\le x\le7\)
\(\sqrt{x-2}+\sqrt{7-x}=2x^2-3x-6\)
\(\Leftrightarrow2x^2-4x-6+\left(2-\sqrt{7-x}\right)+\left(x-2-\sqrt{x-2}\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(2x+2\right)+\dfrac{x-3}{2+\sqrt{7-x}}+\dfrac{\sqrt{x-2}\left(x-3\right)}{\sqrt{x-2}+1}=0\)
\(\Leftrightarrow\left(x-3\right)\left(2x+2+\dfrac{1}{2+\sqrt{7-x}}+\dfrac{\sqrt{x-2}}{\sqrt{x-2}+1}\right)=0\)
\(\Leftrightarrow x=3\) (do \(2x+2+\dfrac{1}{2+\sqrt{7-x}}+\dfrac{\sqrt{x-2}}{\sqrt{x-2}+1}>0;\forall x\in TXĐ\))




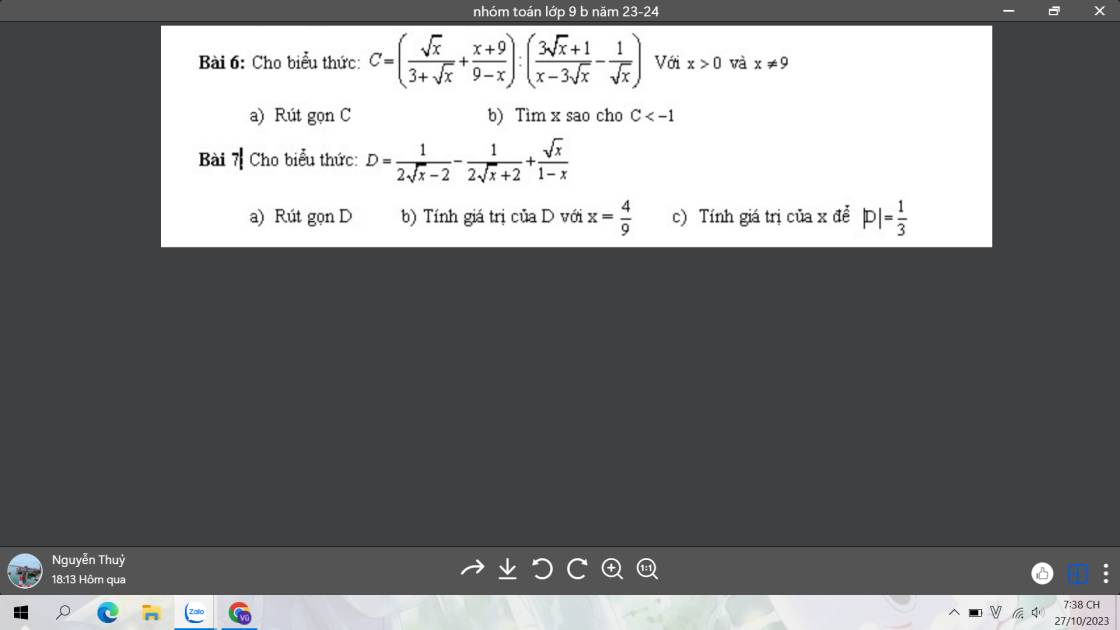 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp
 mn ơi help mình viowis ạ mình đang cần gấp plssssssss
mn ơi help mình viowis ạ mình đang cần gấp plssssssss