\(\dfrac{1}{2^2}>\dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{3^2}>\dfrac{1}{3\cdot4}=\dfrac{1}{3}-\dfrac{1}{4}\)
...
\(\dfrac{1}{100^2}>\dfrac{1}{100\cdot101}=\dfrac{1}{100}-\dfrac{1}{101}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}>\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{2}-\dfrac{1}{101}=\dfrac{99}{202}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{100^2}< \dfrac{1}{99\cdot100}=\dfrac{1}{99}-\dfrac{1}{100}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}=1-\dfrac{1}{100}=\dfrac{99}{100}\)
Suy ra: \(\dfrac{9}{202}< \dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< \dfrac{99}{100}\)
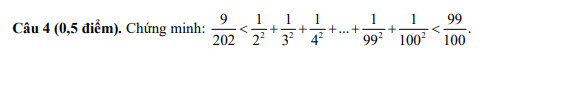
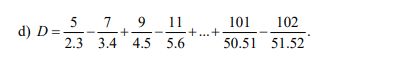
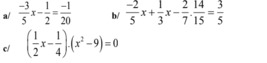
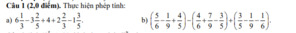
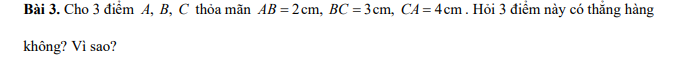
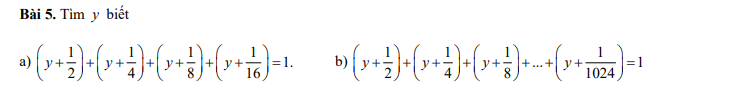
Các bạn làm nhanh và làm đầy đủ, chính xác nha 