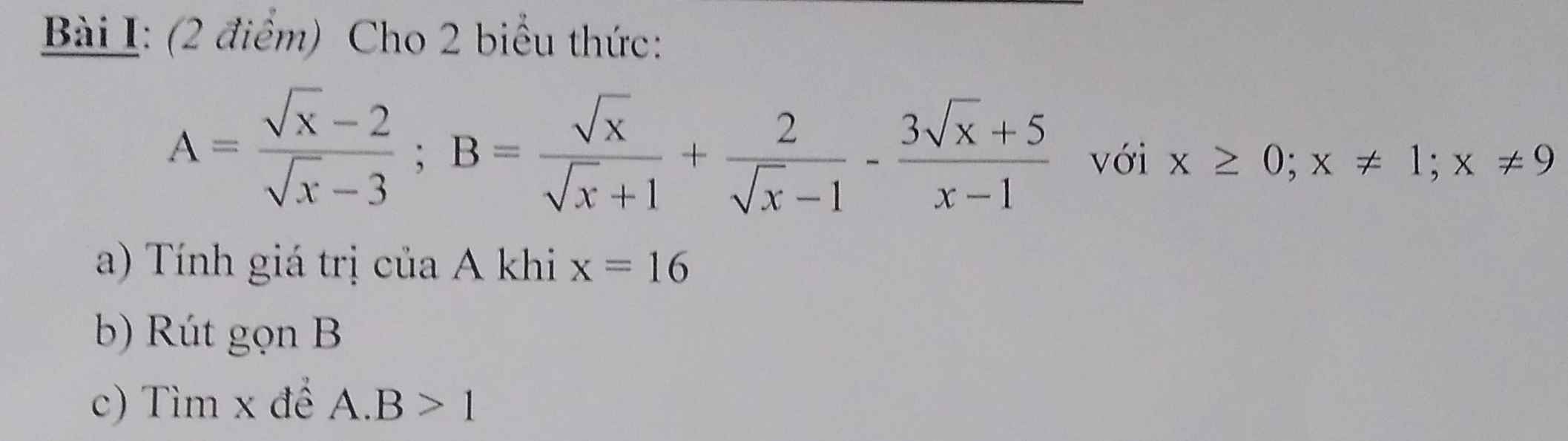a) Thay \(x=16\) vào \(A\), ta được:
\(A=\dfrac{\sqrt{16}-2}{\sqrt{16}-3}=\dfrac{4-2}{4-3}=2\)
b) Ta có \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}+\dfrac{2}{\sqrt{x}-1}-\dfrac{3\sqrt{x}+5}{x-1}\) ĐKXĐ:\(x\ne1;x\ge0\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+2\sqrt{x}+2-3\sqrt{x}-5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1-2\right)\left(\sqrt{x}-1+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)\(=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
c) Ta có \(A.B>1\)
\(\Leftrightarrow2.\dfrac{\sqrt{x}-3}{\sqrt{x}-1}>1\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-6-\sqrt{x}+1}{\sqrt{x}-1}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}-5}{\sqrt{x}-1}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}-5>0\\\sqrt{x}-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}-5< 0\\\sqrt{x}-1< 0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>25\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x< 25\\x< 1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>25\\x< 1\end{matrix}\right.\)
Vậy để \(A.B>1\) thì \(S=\left\{x/0\le x< 1hoặcx>25\right\}\)
a) Thay x=16 vào A, ta được:
\(A=\dfrac{4-2}{4-3}=\dfrac{2}{1}=2\)
b) Ta có: \(B=\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{2}{\sqrt{x}-1}-\dfrac{3\sqrt{x}+5}{x-1}\)
\(=\dfrac{x-\sqrt{x}+2\sqrt{x}+2-3\sqrt{x}-5}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}-3}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\)
c) Để AB>1 thì \(\dfrac{\sqrt{x}-3}{\sqrt{x}-1}-\dfrac{1}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-6-\sqrt{x}+1}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}-5}{2\left(\sqrt{x}-1\right)}>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-5\ge0\\\sqrt{x}-1< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}\ge5\\\sqrt{x}< 1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge25\\x< 1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\ge25\\0\le x< 1\end{matrix}\right.\)