\(A=\dfrac{1}{2^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}\)
\(=\dfrac{1}{2^2}\left(\dfrac{1}{1}+\dfrac{1}{2^2}+...+\dfrac{1}{50^2}\right)\)
=>\(A< \dfrac{1}{2^2}+\dfrac{1}{2^2}\cdot\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)=\dfrac{1}{2^2}+\dfrac{1}{2^2}\cdot\dfrac{49}{50}=\dfrac{99}{200}< \dfrac{1}{2}\)
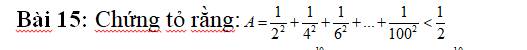



 2 bài này các bạn giúp mik phần d,e,f với
2 bài này các bạn giúp mik phần d,e,f với  còn bài này các bạn giúp mik phần c, h
còn bài này các bạn giúp mik phần c, h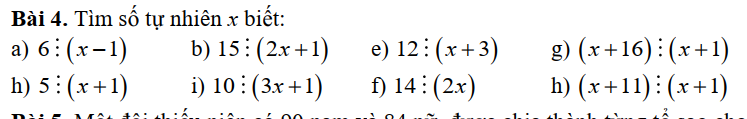 bài này các bạn giúp mik phần g, h, i
bài này các bạn giúp mik phần g, h, i các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp
các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp