Các bạn có biết không, từ ngày 5/8 - 11/8 cứ mỗi 100 bạn bè mời được (và chụp màn hình trước và sau khi mời gửi về cho page) thì bạn nhận được 8 điểm lận đó. Xem chi tiết tại: (1) Cuộc thi Trí tuệ VICE - Bài viết | Facebook. Mời ngay thôi nào!
[Toán.C33|5.8.2021| Hir Dương (Facebook)]
1)

2)

3)
4) 
5) 
#vice
1
đặt biểu thức cần chứng minh là P
có \(\sqrt{a^2+\dfrac{1}{b^2}}=\dfrac{1}{\sqrt{97}}.\sqrt{\left(a^2+\dfrac{1}{b^2}\right).\left(4^2+9^2\right)}\ge\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{b}\right)\)
là tương tự đối với \(\sqrt{b^2+\dfrac{1}{c^2}},\sqrt{c^2+\dfrac{1}{a^2}}\)
\(=>P\ge\)\(\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{b}+4b+\dfrac{9}{c}+4c+\dfrac{9}{a}\right)\)
(đến đây thấy đề sai sai vì ngược dấu )
à em nhầm chút ko để ý
1 đặt biểu thức là P
\(=>\sqrt{a^2+\dfrac{1}{b^2}}=\dfrac{1}{\sqrt{97}}\sqrt{\left(a^2+\dfrac{1}{b^2}\right)\left(4^2+9^2\right)}\ge\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{b}\right)\)
làm tương tự với \(\sqrt{b^2+\dfrac{1}{c^2}},\sqrt{c^2+\dfrac{1}{a^2}}\)
\(=>P\ge\dfrac{1}{\sqrt{97}}\left(4a+\dfrac{9}{a}+4b+\dfrac{9}{b}+4c+\dfrac{9}{c}\right)\)
có \(4a+\dfrac{9}{a}=4a+\dfrac{16}{9a}+\dfrac{65}{9a}\ge2\sqrt{\dfrac{4.16}{9}}+\dfrac{81}{9a}=\dfrac{16}{3}+\dfrac{65}{9a}\)
làm tương tự với \(4b+\dfrac{9}{b},4c+\dfrac{9}{c}\)
\(=>P\ge\dfrac{1}{\sqrt{97}}\left(\dfrac{16}{3}+\dfrac{16}{3}+\dfrac{16}{3}+\dfrac{65}{9a}+\dfrac{65}{9b}+\dfrac{65}{9c}\right)\)
\(=\dfrac{1}{\sqrt{97}}\left(16+\dfrac{\left(\sqrt{65}+\sqrt{65}+\sqrt{65}\right)^2}{9\left(a+b+c\right)}\right)=\dfrac{1}{\sqrt{97}}\left(16+\dfrac{585}{9.2}\right)=\dfrac{\sqrt{97}}{2}\)
dấu"=" xảy ra<=>a=b=c=2/3
Làm câu hệ vậy+((
C33.4:
Ta có: \(\left\{{}\begin{matrix}x^2+y^2=1\left(1\right)\\21x+3y+48x^2-48y^2+28xy=69\left(2\right)\end{matrix}\right.\)
Từ pt (1) ta có: \(x^2+y^2=1\Rightarrow y^2=1-x^2\)
Thay vào pt (2) ta được: \(21x+3\sqrt{1-x^2}+48x^2-48\left(1-x^2\right)+28x\sqrt{1-x^2}-69=0\)
\(\Leftrightarrow3\sqrt{\left(1-x\right)\left(1+x\right)}+28x\sqrt{\left(1-x\right)\left(1+x\right)}-21\sqrt{\left(1-x\right)\left(1-x\right)}-48\left(1-x^2\right)-48\left(1-x^2\right)=0\)
\(\Leftrightarrow\sqrt{1-x}\left(3\sqrt{1+x}+28x\sqrt{1+x}-21\sqrt{1-x}-96\left(1+x\right)\sqrt{1-x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{1-x}=0\\3\sqrt{1+x}+28x\sqrt{1+x}-21\sqrt{1-x}-96\left(1+x\right)\sqrt{1-x}=0\end{matrix}\right.\)
+ Nếu \(\sqrt{1-x}=0\Leftrightarrow1-x=0\Leftrightarrow x=1\Rightarrow y=0\)
+Nếu \(3\sqrt{1+x}+28x\sqrt{1+x}-21\sqrt{1-x}-96\left(1+x\right)\sqrt{1-x}=0\)
\(\Leftrightarrow3\sqrt{1+x}+28x\sqrt{1+x}=21\sqrt{1-x}+96\left(1+x\right)\sqrt{1-x}\)
\(\Leftrightarrow784x^3+952x^2+177x+9=-9216x^3-13248x^2+8775x+13689\)
\(\Leftrightarrow10000x^3+14200x^2-8598x-13680=0\)
\(\Leftrightarrow x=\dfrac{24}{25}\Rightarrow y=\dfrac{7}{25}\)
Thay \(x=\dfrac{24}{24};y=\dfrac{7}{25}\) vào hệ pt ta thấy thoả mãn
\(x=\dfrac{24}{25};y=\dfrac{7}{25}\) là 1 cặp nghiệm của hệ pt
Vậy hệ pt có nghiệm: \(\left(x;y\right)\in\left\{\left(\dfrac{24}{25};\dfrac{7}{25}\right),\left(1;0\right)\right\}\)
Đăng giờ thiêng thật đấy, tắt máy lúc 10:45 thì đăng lúc 10:47 :"))




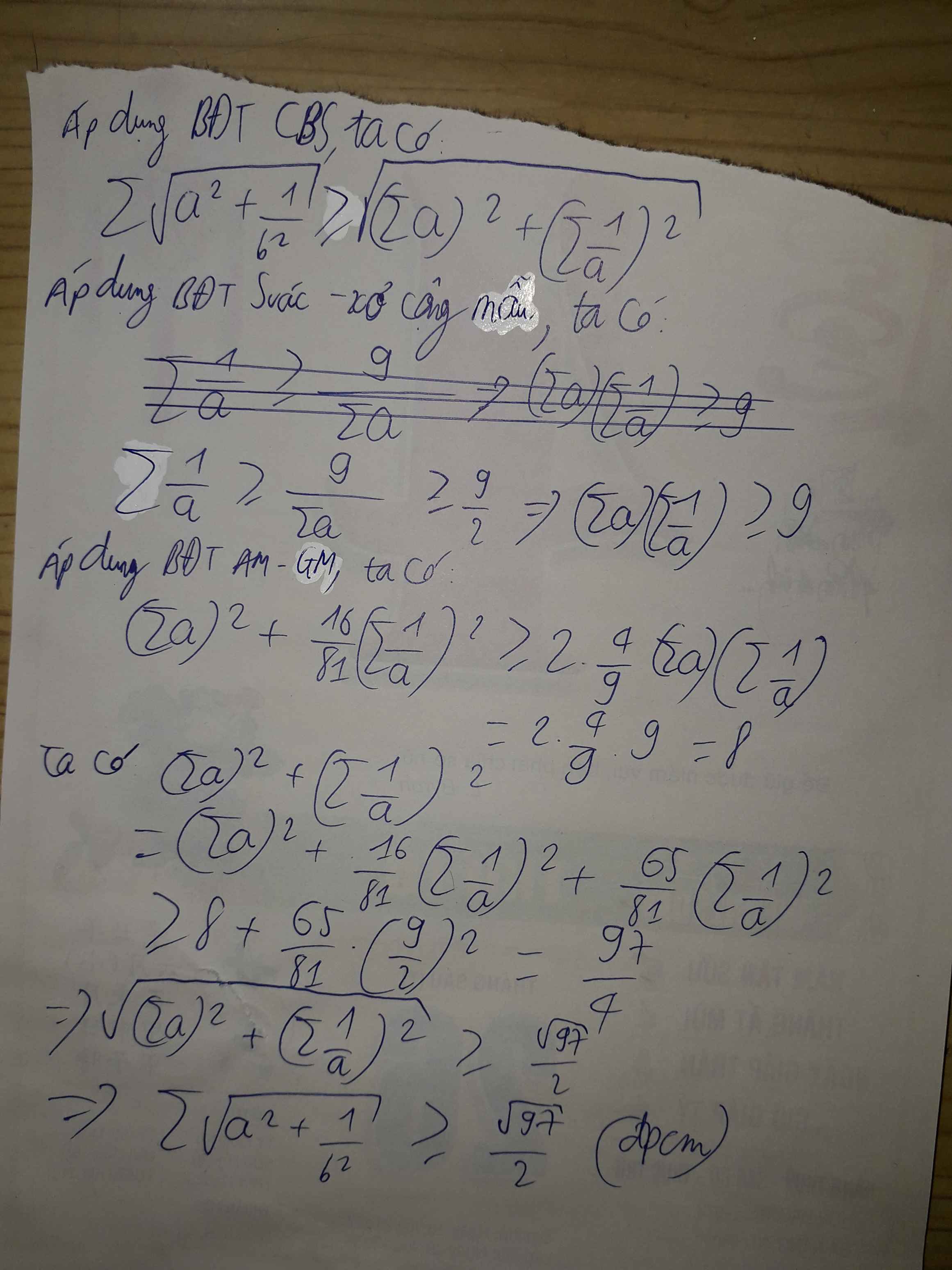

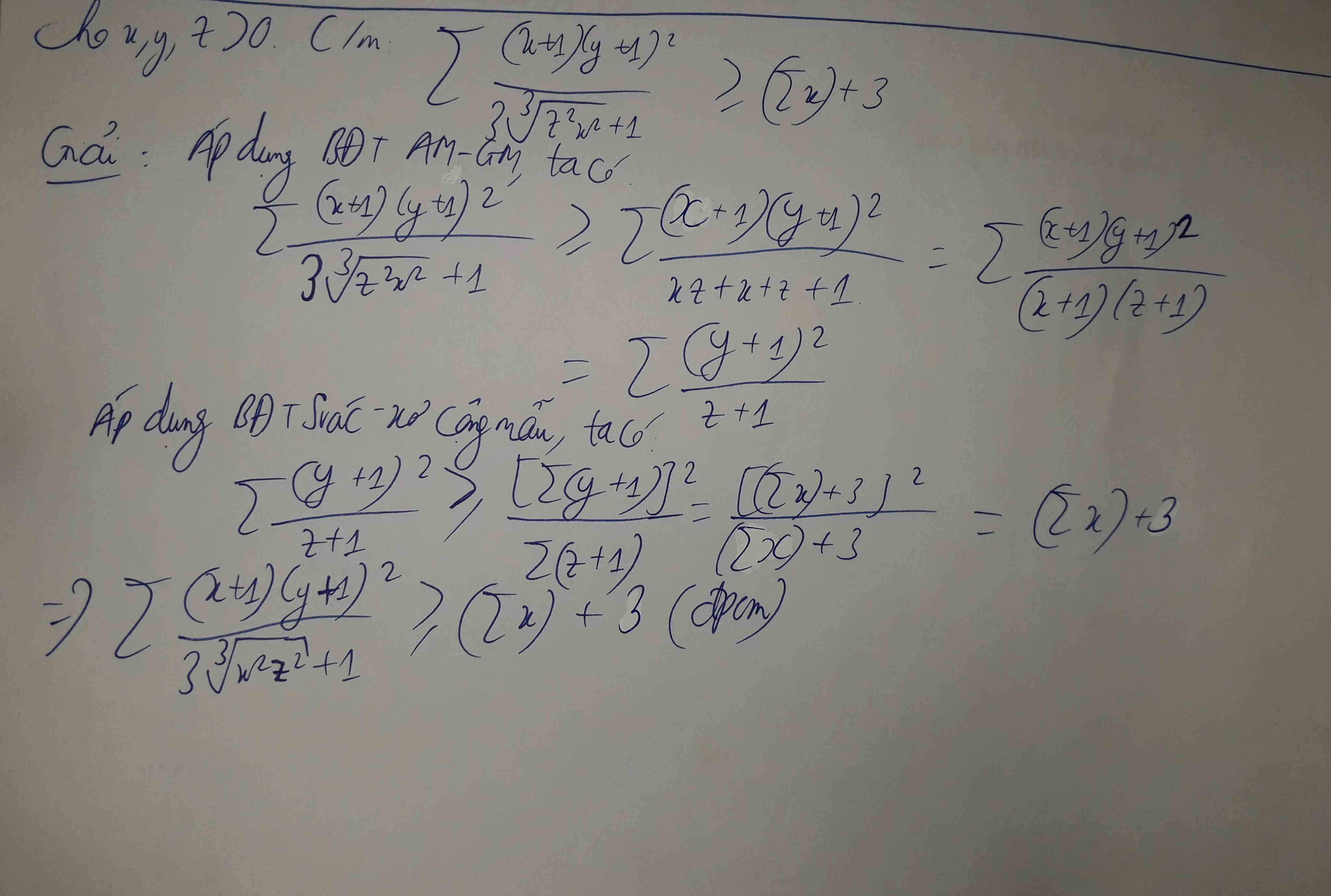




























 (3-4 điểm thưởng/ý làm)
(3-4 điểm thưởng/ý làm)