Hãy hỗ trợ chúng mình đạt 20.000 like page! Cuộc thi Trí tuệ VICE | Facebook
[Toán.C15 _ 1.8.2021 | Hir Dương (Facebook)]
1)

2)

3)

4)

5)

C15. 5:
Áp dụng BĐT Cauchy:
\(\dfrac{a^3}{\left(1+b\right)\left(1+c\right)}+\dfrac{1+b}{8}+\dfrac{1+c}{8}\ge3\sqrt[3]{\dfrac{a^3\left(1+b\right)\left(1+c\right)}{\left(1+b\right)\left(1+c\right).64}}=\dfrac{3a}{4}\)
\(\Rightarrow\dfrac{a^3}{\left(1+b\right)\left(1+c\right)}\ge\dfrac{3a}{4}-\dfrac{b+1}{8}-\dfrac{c+1}{8}\)
Tương tự: \(\Rightarrow\dfrac{b^3}{\left(1+c\right)\left(1+a\right)}\ge\dfrac{3b}{4}-\dfrac{c+1}{8}-\dfrac{a+1}{8}\); \(\Rightarrow\dfrac{c^3}{\left(1+b\right)\left(1+a\right)}\ge\dfrac{3c}{4}-\dfrac{b+1}{8}-\dfrac{a+1}{8}\)
Cộng theo vế: \(VT\ge\dfrac{3}{4}\left(a+b+c\right)-\dfrac{1}{4}\left(a+b+c\right)-\dfrac{3}{4}=\dfrac{a+b+c}{2}-\dfrac{3}{4}\ge\dfrac{3\sqrt[3]{abc}}{2}-\dfrac{3}{4}=\dfrac{3}{4}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=1\)
C15.2: ( Trần Văn Khắnk - Trần Thanh Fuongzz)
Theo định lý Sin: \(\dfrac{a}{sinA}=2R\Rightarrow sinA=\dfrac{a}{2R}\Rightarrow S=\dfrac{1}{2}bc.sinA=\dfrac{abc}{4R}\Leftrightarrow abc=4SR\) (1)
Gọi G là trọng tâm của tam giác ABC, ta có:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\Leftrightarrow3\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
\(\Leftrightarrow9OG^2=OA^2+OB^2+OC^2+2\overrightarrow{OA}.\overrightarrow{OB}+2\overrightarrow{OB}.\overrightarrow{OC}+2\overrightarrow{OC}.\overrightarrow{OA}\)
\(\Leftrightarrow9OG^2=3R^2+2\overrightarrow{OA}.\overrightarrow{OB}+2\overrightarrow{OB}.\overrightarrow{OC}+2\overrightarrow{OC}.\overrightarrow{OA}\)
Có \(2\overrightarrow{OA}.\overrightarrow{OB}=\overrightarrow{OA}^2+\overrightarrow{OB}^2-\left(\overrightarrow{OA}-\overrightarrow{OB}\right)^2=2R^2-c^2\)
Tương tự suy ra: \(9OG^2=9R^2-\left(a^2+b^2+c^2\right)\Rightarrow a^2+b^2+c^2=9\left(R^2-OG^2\right)\) (2)
Từ (1) và (2), ta có đpcm \(\Leftrightarrow12SR\ge4S\sqrt{9\left(R^2-OG^2\right)}\)
\(\Leftrightarrow R\ge\sqrt{R^2-OG^2}\)
\(\Leftrightarrow OG^2\ge0\) ( luôn đúng )
Dấu "=" xảy ra khi và chỉ khi \(O\equiv G\) hay tam giác ABC đều.
C15.3:
\(3=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge\dfrac{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}{3}\Leftrightarrow3\ge\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\Leftrightarrow abc\ge1\)
Khi đó: \(\dfrac{1}{1+\sqrt{\left(a+b\right)^3+abc}}\le\dfrac{1}{1+\sqrt{\left(a+b\right)^3+1}}=\dfrac{1-\sqrt{\left(a+b\right)^3+1}}{1-\left(a+b\right)^3-1}=\dfrac{\sqrt{\left(a+b\right)^3+1}-1}{\left(a+b\right)^3}\)
Xét \(\sqrt{\left(a+b\right)^3+1}=\sqrt{\left(a+b+1\right)\left[\left(a+b\right)^2-\left(a+b\right)+1\right]}\le\dfrac{a+b+1+\left(a+b\right)^2-\left(a+b\right)+1}{2}=\dfrac{\left(a+b\right)^2}{2}+1\)
\(\Rightarrow\dfrac{\sqrt{\left(a+b\right)^3+1}-1}{\left(a+b\right)^3}\le\dfrac{\left(a+b\right)^2}{2.\left(a+b\right)^3}=\dfrac{1}{2}.\dfrac{1}{a+b}\le\dfrac{1}{8}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\)
Tương tự với 2 phân thức còn lại ta có:
\(VT\le\dfrac{1}{8}\left(\dfrac{2}{a}+\dfrac{2}{b}+\dfrac{2}{c}\right)\le\dfrac{1}{4}\cdot\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le\dfrac{3}{4}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=1\)




 )
)




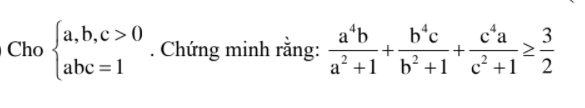
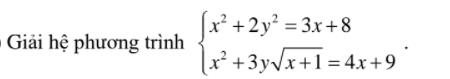
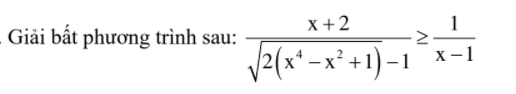

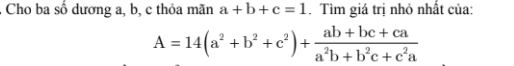
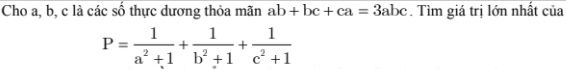
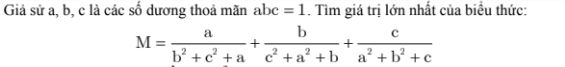




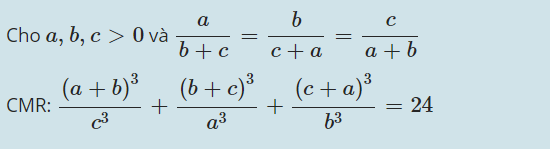
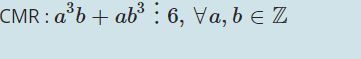
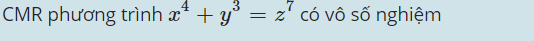

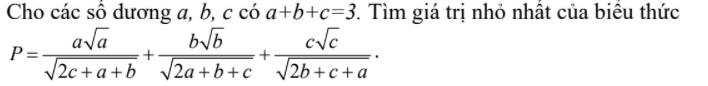

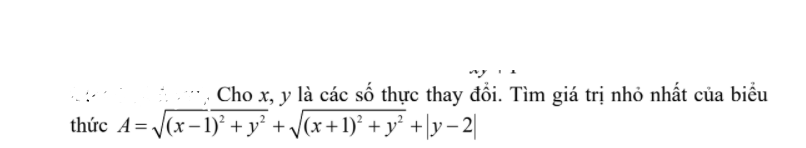
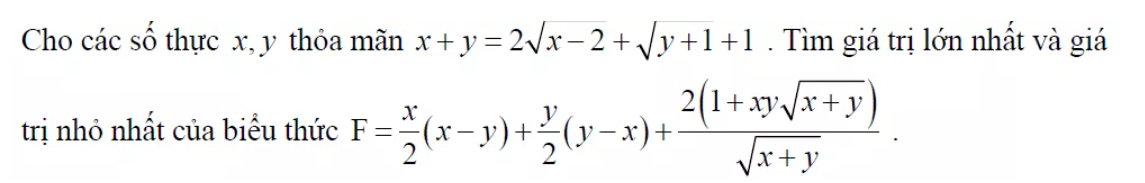
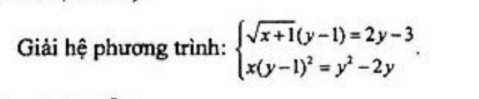
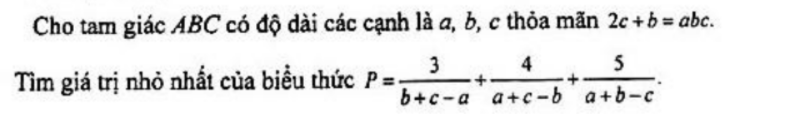
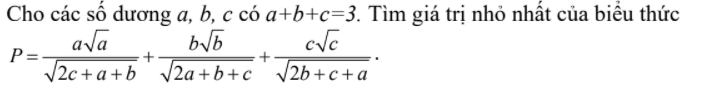
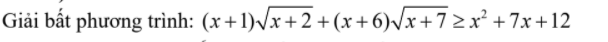

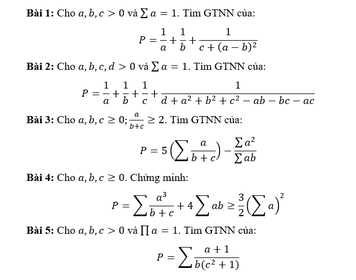



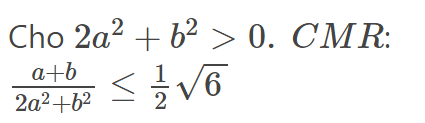
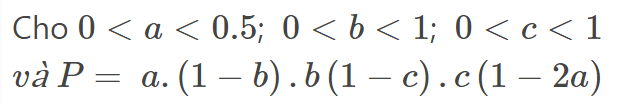
 4)
4)