Xem bài viết Facebook và đóng góp share, like tại: Cuộc thi Trí tuệ VICE - Bài viết | Facebook giúp chúng mình nha!

 (3-4 điểm thưởng/ý làm)
(3-4 điểm thưởng/ý làm)
C7, \(\dfrac{\left(b+c\right)\left(a^2+bc\right)}{b^2+bc+c^2}\ge\dfrac{\left(2\sqrt{bc}\right).\left(2a\sqrt{bc}\right)}{3\sqrt[3]{b^2.bc.c^2}}=\dfrac{4abc}{3abc}=\dfrac{4}{3}\left(1\right)\)
tương tự \(=>\dfrac{\left(a+c\right)\left(b^2+Ac\right)}{a^2+ac+c^2}\ge\dfrac{4}{3}\left(2\right)\)
\(=>\dfrac{\left(b+a\right)\left(c^2+ba\right)}{a^2+ab+b^2}\ge\dfrac{4}{3}\left(3\right)\)
cộng vế (1)(2)(3) \(=>P\ge4\)
dấu"=" xảy ra<=>a=b=c=1
ằng một đoạn văn khoảng 8 câu, em hãy trình bày cảm nhận của mình về nhân vật Mèo trong truyện Bức tranh của em gái tôi. Trong đoạn văn, có sử dụng một phép so sánh (yêu cầu gạch chân câu có phép so sánh đó và chú thích rõ)
C10
quy đồng Q\(=>Q=\dfrac{x^3\left(x+2\right)+y^3\left(y+2\right)}{4\left(x+2\right)\left(y+2\right)}\)
\(=>Q=\dfrac{x^4+y^4+2\left(x^3+y^3\right)}{4\left(x+2\right)\left(y+2\right)}=\dfrac{x^4+y^4+2\left(x+y\right)\left(x^2-xy+y^2\right)}{4\left(x+2\right)\left(y+2\right)}\)
\(Q\ge\dfrac{2x^2y^2+2\left(x+y\right)\left(2xy-xy\right)}{4xy+8x+8y+16}\)\(=\dfrac{2x^2y^2+2\left(x+y\right)xy}{4\left(4+2x+2y+4\right)}\)
\(=\dfrac{xy\left[2xy+2\left(x+y\right)\right]}{4[2\left(x+y\right)+8]}=\dfrac{4[2\left(x+y\right)+8]}{4[2\left(x+y\right)+8]}=1\)
dấu"=" xảy ra<=>x=y=2
\(\)
C8:
1) Làm cách dài:(
Đặt \(t=a+b+c\Rightarrow t^2=a^2+b^2+c^2+2\)
Ta có:A= \(\dfrac{a}{b^2+c^2+2}+\dfrac{b}{c^2+a^2+2}+\dfrac{c}{a^2+b^2+2}=\dfrac{a^2}{at^2-a^3}+\dfrac{b^2}{bt^2-b^3}+\dfrac{c^2}{ct^2-c^3}\)
Áp dụng BĐT Cauchy Schwars dạng Engel, ta được:
A\(\ge\dfrac{\left(a+b+c\right)^2}{at^2+bt^2+ct^2-a^3-b^3-c^3}=\dfrac{t^2}{t^3-\left(a^3+b^3+c^3\right)}=\dfrac{t^3}{t^4-t\left(a^3+b^3+c^3\right)}=\dfrac{t^3}{t^4-\left(a+b+c\right)\left(a^3+b^3+c^3\right)}\)
Cm: \(\left(a+b+c\right)\left(a^3+b^3+c^3\right)\ge\left(a^2+b^2+c^2\right)^2\)
Thật vậy: \(a^3+b^3+c^3=\dfrac{a^4}{a}+\dfrac{b^4}{b}+\dfrac{c^4}{c}\ge\dfrac{\left(a^2+b^2+c^2\right)^2}{a+c+b}\Rightarrow\left(a+b+c\right)\left(a^3+b^3+c^3\right)\ge\left(a^2+b^2+c^2\right)^2\)
\(\Rightarrow A\ge\dfrac{t^3}{t^4-\left(a^2+b^2+c^2\right)^2}=\dfrac{t^3}{t^4-\left(t^2-2\right)^2}=\dfrac{t^3}{4t^2-4}\)
Ta cần cm: \(\dfrac{t^3}{4t^2-4}\ge\dfrac{3\sqrt{3}}{8}\)
Thật vậy: \(8t^3-12\sqrt{3}t^2+12\sqrt{3}\ge0\Leftrightarrow4\left(2t+\sqrt{3}\right)\left(t-\sqrt{3}\right)^2\ge0\) (Đúng với mọi \(t\ge\sqrt{3}\))
=> Đpcm.
P/s: Cảm ơn anh Quân giúp đỡ em nha:3










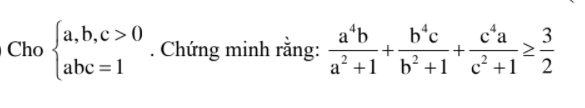
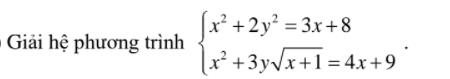
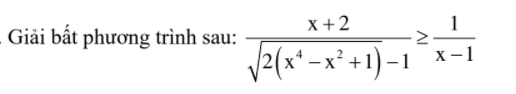
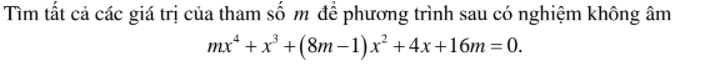

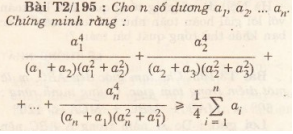
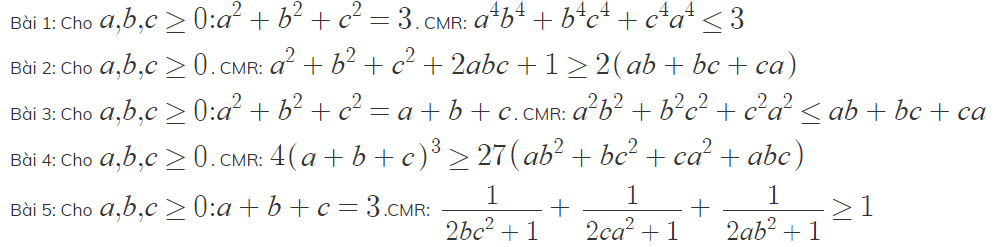
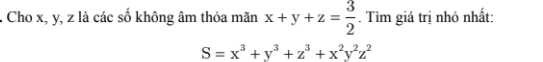
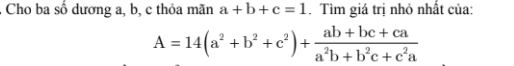
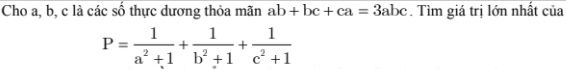
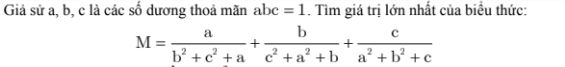




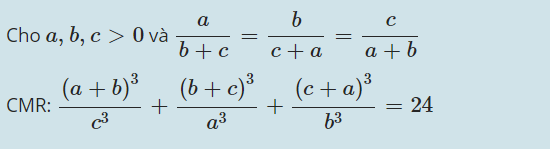
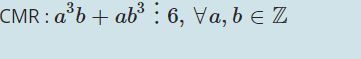
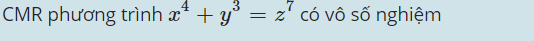

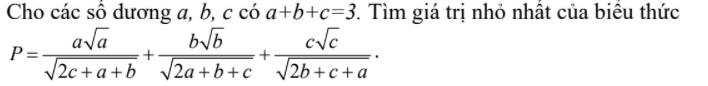

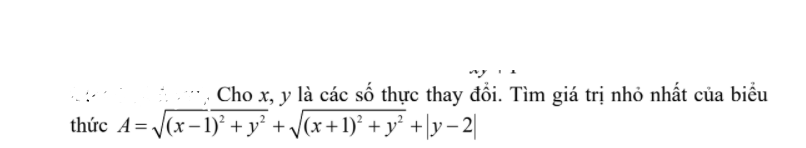
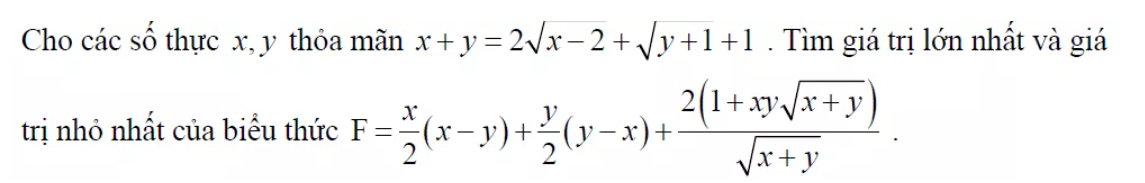
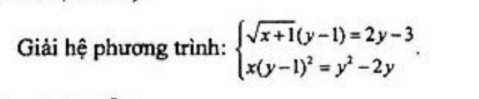
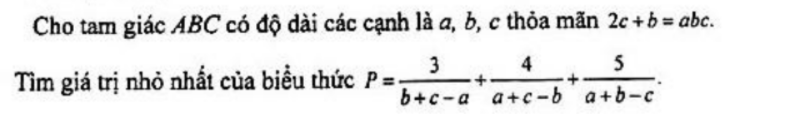
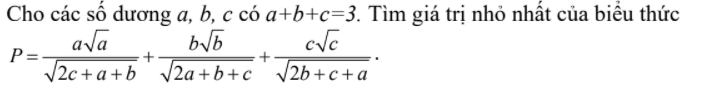
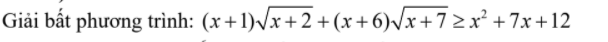

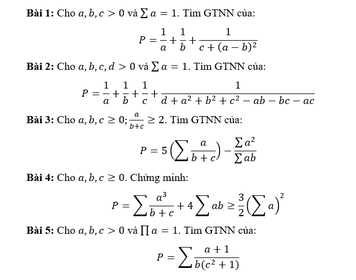



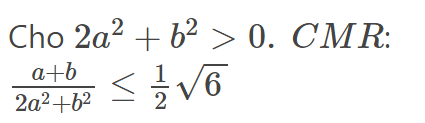
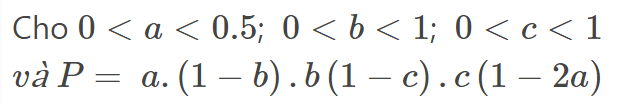
 4)
4)