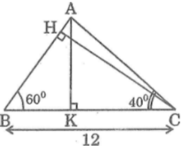
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-60^0-45^0=75^0\)
Xét ΔABC có \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{AC}{sin60}=\dfrac{AB}{sin45}=\dfrac{12}{sin75}=12\sqrt{6}-12\sqrt{2}\)
=>\(\left\{{}\begin{matrix}AC=\left(12\sqrt{6}-12\sqrt{2}\right)\cdot sin60=18\sqrt{2}-6\sqrt{6}\left(cm\right)\\AB=\left(12\sqrt{6}-12\sqrt{2}\right)\cdot sin45=12\sqrt{3}-12\left(cm\right)\end{matrix}\right.\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC\)
\(=\dfrac{1}{2}\cdot\left(12\sqrt{3}-12\right)\cdot12\cdot sin60=\left(6\sqrt{3}-6\right)\cdot12\cdot\dfrac{\sqrt{3}}{2}\)
\(=6\left(\sqrt{3}-1\right)\cdot6\sqrt{3}=36\sqrt{3}\left(\sqrt{3}-1\right)=108-36\sqrt{3}\left(cm^2\right)\)
Xét $\triangle ABC$ có $\hat{A} + \hat{B} + \hat{C} = 180^o$
$\Rightarrow \hat{A} = 180^o - 60^o - 45^o = 75^o$
Xét $\triangle ABC$ có $\dfrac{BC}{\sin A} = \dfrac{AC}{\sin B} = \dfrac{AB}{\sin C}$
$\Rightarrow \dfrac{AC}{\sin 60^o} = \dfrac{AB}{\sin 45^o} = \dfrac{12}{\sin 75^o} = 12\sqrt{6} - 12\sqrt{2}$
$\Rightarrow \begin{cases}
AC = (12\sqrt{6} - 12\sqrt{2}) \cdot \sin 60^o = 18\sqrt{2} - 6\sqrt{6} (cm) \\
AB = (12\sqrt{6} - 12\sqrt{2}) \cdot \sin 45^o = 12\sqrt{3} - 12 (cm)
\end{cases}$
Diện tích tam giác ABC là:
$S_{ABC} = \dfrac{1}{2} \cdot BA \cdot BC \cdot \sin ABC$
$= \dfrac{1}{2} \cdot (12\sqrt{3} - 12) \cdot 12 \cdot \sin 60^o = (6\sqrt{3} - 6) \cdot 12 \cdot \dfrac{\sqrt{3}}{2}$
$= 6(\sqrt{3} - 1) \cdot 6\sqrt{3} = 36\sqrt{3}(\sqrt{3} - 1) = 108 - 36\sqrt{3} (cm^2)$