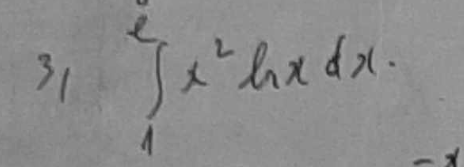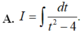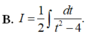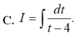Đặt \(\left\{{}\begin{matrix}\ln x=u\Rightarrow\dfrac{1}{x}dx=du\\dv=x^2dx\Rightarrow v=\dfrac{1}{3}x^3\end{matrix}\right.\)
Ta có: \(\int\limits^e_1x^2.\ln x=\dfrac{1}{3}x^3.\ln x|^e_1-\int\limits^e_1\dfrac{1}{3}x^2=\dfrac{e^3}{3}-\dfrac{1}{9}x^3|^e_1=\dfrac{e^3}{3}-\dfrac{e^3}{9}+\dfrac{1}{9}=\dfrac{2e^3}{9}+\dfrac{1}{9}\)