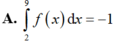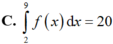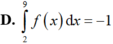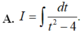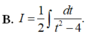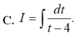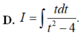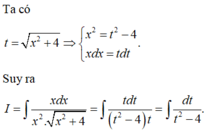Các câu hỏi tương tự
Tính nguyên hàm
I
∫
d
x
x
x
2
+
4
bằng cách đặt
t
x
2
+
4
, mệnh đề nào dưới đây đúng? A.
I
∫
d...
Đọc tiếp
Tính nguyên hàm I = ∫ d x x x 2 + 4 bằng cách đặt t = x 2 + 4 , mệnh đề nào dưới đây đúng?
A. I = ∫ d t t 2 − 4 .
B. I = 1 2 ∫ d t t 2 − 4 .
C. I = ∫ d t t − 4 .
D. I = ∫ t d t t 2 − 4 .
Tính tích phân
I
∫
0
1
2
4
−
x
2
d
x
bằng cách đặt x2sint. Mệnh đề nào dưới đây đúng? A.
I
2
∫
0
1
d
t
B.
I
2
∫
0...
Đọc tiếp
Tính tích phân I = ∫ 0 1 2 4 − x 2 d x bằng cách đặt x=2sint. Mệnh đề nào dưới đây đúng?
A. I = 2 ∫ 0 1 d t
B. I = 2 ∫ 0 π 6 d t
C. I = ∫ 0 π 3 d t
D. I = ∫ 0 π 6 d t
Tìm nguyên hàm của
I
∫
2
x
x
2
−
1
d
x
bằng cách đặt
u
x
2
−
1
, mệnh đề nào dưới đây đúng? A.
I
2
∫
u
d
u
B.
I
∫
2
u
d...
Đọc tiếp
Tìm nguyên hàm của I = ∫ 2 x x 2 − 1 d x bằng cách đặt u = x 2 − 1 , mệnh đề nào dưới đây đúng?
A. I = 2 ∫ u d u
B. I = ∫ 2 u d u
C. I = ∫ u d u
D. I = 1 2 ∫ u d u
Tính tích phân Iintlimits^{pi}_0x^2cos2xdx bằng cách đặt left{{}begin{matrix}ux^2dvcos2xdxend{matrix}right..Mệnh đề nào dưới đây đúng?A. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}-intlimits^{pi}_0xsin2xdxB. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}-2intlimits^{pi}_0xsin2xdxC. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}+intlimits^{pi}_0xsin2xdxD. Idfrac{1}{2}x^2sin2x|^{^{pi}_0}+2intlimits^{pi}_0xsin2xdx
Đọc tiếp
Tính tích phân I=\(\int\limits^{\pi}_0\)\(x^2cos2xdx\) bằng cách đặt \(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\).Mệnh đề nào dưới đây đúng?
A. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-\int\limits^{\pi}_0xsin2xdx\)
B. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-2\int\limits^{\pi}_0xsin2xdx\)
C. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+\int\limits^{\pi}_0xsin2xdx\)
D. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+2\int\limits^{\pi}_0xsin2xdx\)
Cho hàm số yf(x). Hàm số y f’(x) có đồ thị như hình vẽ dưới đây. Đặt
g
(
x
)
2
f
(
x
)
-
x
+
1
2
.Biết f(-2)f(3). Mệnh đề nào đúng? A. B C. D.
Đọc tiếp
Cho hàm số y=f(x). Hàm số y= f’(x) có đồ thị như hình vẽ dưới đây.
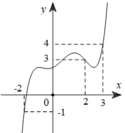
Đặt g ( x ) = 2 f ( x ) - x + 1 2 .Biết f(-2)=f(3). Mệnh đề nào đúng?
A. ![]()
B![]()
C. ![]()
D. ![]()
Cho hàm số y f( x) liên tục trên R Đồ thị của hàm số y f’ (x) như hình bên. Đặt g(x) 2f(x)-(x+ 1) 2 . Mệnh đề nào dưới đây đúng? A.
m
i
n
[
-
3
;
3
]
g
(
x
)
g
(
1
)
.
B.
m...
Đọc tiếp
Cho hàm số y= f( x) liên tục trên R Đồ thị của hàm số y= f’ (x) như hình bên. Đặt g(x) = 2f(x)-(x+ 1) 2 . Mệnh đề nào dưới đây đúng?
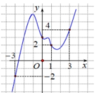
A. m i n [ - 3 ; 3 ] g ( x ) = g ( 1 ) .
B. m a x [ - 3 ; 3 ] g ( x ) = g ( 1 ) .
C. m i n [ - 3 ; 3 ] g ( x ) = g ( 3 ) .
D. Không tồn tại giá trị nhỏ nhất của g( x) trên [-3;3]
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
1
x
-
1
thỏa mãn F(5) 2 và F(0) 1. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = 1 x - 1 thỏa mãn F(5) = 2 và F(0) = 1. Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()
![]()
Cho hàm số yf(x). Đồ thị của hàm số yf (x) như hình vẽ. Đặt h(x)f(x)-x. Mệnh đề nào dưới đây đúng? A. . B. . C. . D. .
Đọc tiếp
Cho hàm số y=f(x). Đồ thị của hàm số y=f '(x) như hình vẽ. Đặt h(x)=f(x)-x. Mệnh đề nào dưới đây đúng?
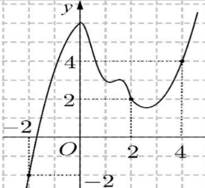
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hàm số y f(x) liên tục trên [2;9]. F(x) là một nguyên hàm của hàm số f(x) trên [2;9] và F(2) 5; F(9) 4. Mệnh đề nào sau đây đúng?
Đọc tiếp
Hàm số y = f(x) liên tục trên [2;9]. F(x) là một nguyên hàm của hàm số f(x) trên [2;9] và F(2) = 5; F(9) = 4. Mệnh đề nào sau đây đúng?