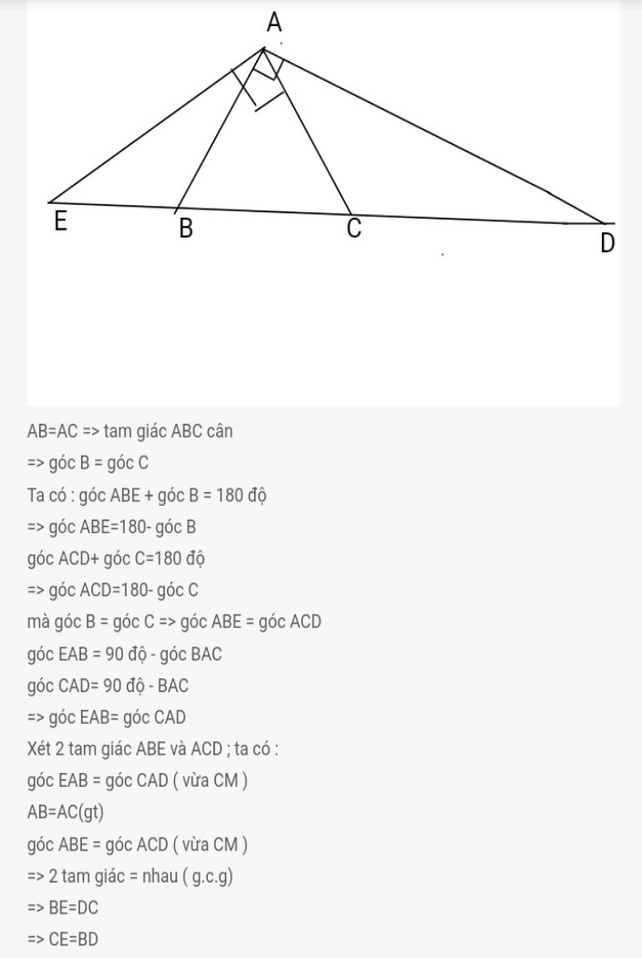
a) Vì tam giác ABC có AB=AC
=> ∆ABC cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\)
b) Ta có: \(\left\{{}\begin{matrix}\widehat{ABE}+\widehat{ABC}=180^o\\\widehat{ACD}+\widehat{ACD}=180^o\end{matrix}\right.\)
Mà \(\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{ABE}=\widehat{ACD}\)
Lại có: \(\widehat{EAB}+\widehat{BAC}=90^o\)
\(\widehat{DAC}+\widehat{CAB}=90^o\)
=> \(\widehat{EAB}=\widehat{DAC}\)
Xét ∆EAB và ∆DAC:
AB=AC(gt)
\(\widehat{EAB}=\widehat{DAC}\left(cmt\right)\)
\(\widehat{ABE}=\widehat{ACD}\left(cmt\right)\)
=> ∆EAB=∆DAC(g.c.g)
=> EB=CD(2 cạnh t/ứ)
=> EB+BC=DC+BC
=> EC=BD
=> Đpcm
a) Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)
a) Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Suy ra: ˆABC=ˆACBABC^=ACB^(hai góc ở đáy)
b) xét ΔAEC và ΔADB (^EAC=^BAD=90 độ) có:
\(\left\{{}\begin{matrix}AB=AC\\gócABC=gócACB\end{matrix}\right.\)
⇒ΔAEC = ΔADB
⇒BD=CE