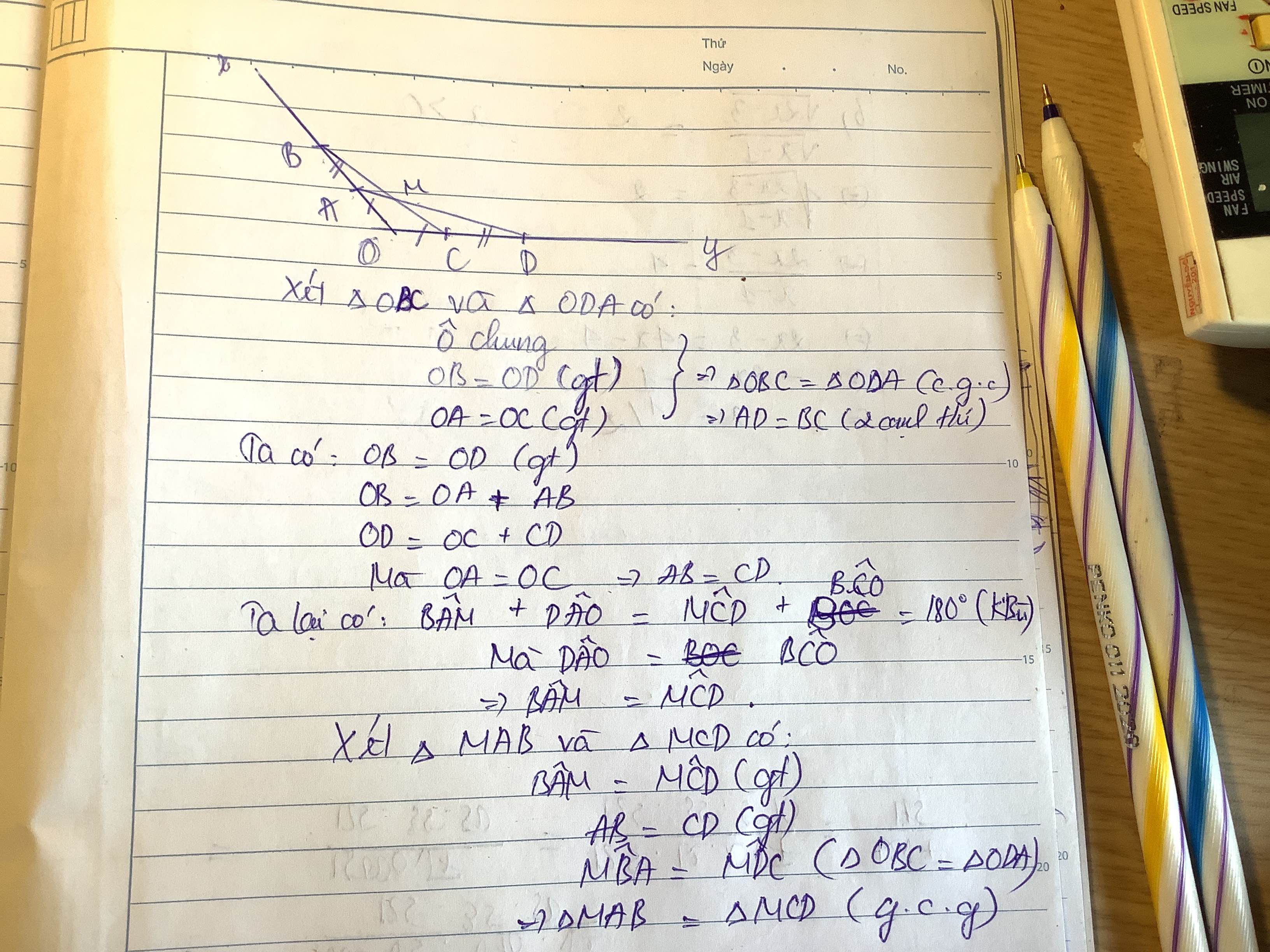a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{COB}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOCB
nên \(\widehat{OAD}=\widehat{OCB}\)
mà \(\widehat{MAB}=180^0-\widehat{OAD}\)
và \(\widehat{MCD}=180^0-\widehat{OCB}\)
nên \(\widehat{MAB}=\widehat{MCD}\)
Xét ΔMAB và ΔMCD có
\(\widehat{MAB}=\widehat{MCD}\)
AB=CD
\(\widehat{MBA}=\widehat{MDC}\)
Do đó: ΔMAB=ΔMCD