Question

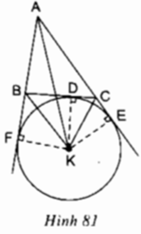
Bài 4: Cho tam giác ABC có ba góc nhọn và đường cao BE. Gọi H và K lần lượt là chân các đường vuông góc kẻ từ điểm E đến các đường thẳng AB và BC.
1) Chứng minh tứ giác BHEK là tứ giác nội tiếp
2) Chứng minh BH.BA = BK.BC
3) Gọi F là chân đường vuông góc kẻ từ điểm C đến đường thẳng AB và I là trung điểm  của đoạn thẳng EF. Chứng minh ba điểm H, I, K là ba điểm thẳng hàng.

 

Answer 1

1: Xét tứ giác BHEK có \(\widehat{BHE}+\widehat{BKE}=180^0\)

nên BHEK là tứ giác nội tiếp

2: Xét ΔBEA vuông tại E có EH là đường cao

nên \(BH\cdot BA=BE^2\left(1\right)\)

Xét ΔBEC vuông tại E có EK là đường cao

nên \(BK\cdot BC=BE^2\left(2\right)\)

Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)