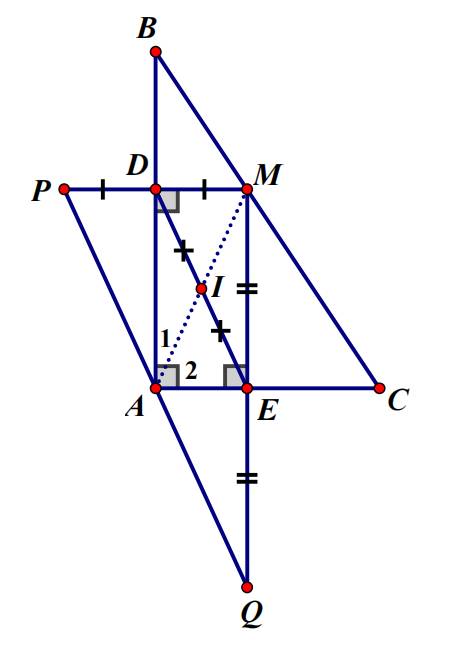
Bài 3 (3 điểm). Cho tam giác ABC vuông tại A (AB < AC) , đường cao AH. M là trung điểm BC. Vẽ MD song song với AC (D thuộc AB), ME song song với AB (E thuộc AC) a) Cho AB = 6cm, BC = 10cm tính AC. b) Chứng minh tứ giác ADME là hình chữ nhật. c) Chứng minh rằng BDEM là hình bình hành. d) Trên tia đối EB lấy K sao cho EB = EK Trên tia đối EM lấy I sao cho EM = EI Chứng minh ba điểm A; I; K thẳng hàng.
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+6^2=10^2\)
=>\(AC^2=100-36=64\)
=>\(AC=\sqrt{64}=8\left(cm\right)\)
b: Xét tứ giác ADME có
AD//ME
AE//MD
Do đó: ADME là hình bình hành
Hình bình hành ADME có \(\widehat{DAE}=90^0\)
nên ADME là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{1}{2}BC\)
Ta có: DE//BC
M\(\in\)BC
Do đó: DE//MB
Ta có: \(DE=\dfrac{1}{2}BC\)
\(MC=MB=\dfrac{1}{2}BC\)
Do đó: DE=MC=MB
Xét tứ giác BDEM có
DE//MB
DE=MB
Do đó: BDEM là hình bình hành
d: Xét tứ giác ABCK có
E là trung điểm chung của AC và BK
=>ABCK là hình bình hành
=>AK//BC
Xét tứ giác AMCI có
E là trung điểm chung của AC và MI
=>AMCI là hình bình hành
=>AI//CM
=>AI//BC
Ta có: AI//BC
AK//BC
AI,AK có điểm chung là A
Do đó: A,I,K thẳng hàng