Bài 20: Cho tam giác ABC vuông tại A, D là trung điểm BC. Gọi M là điểm đối xứng của D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng của D qua AC, F là giao điểm của DN và AC. a/ Tứ giác AEDF là hình gì ? Vì sao ? b/ Các tứ giác ADBM, ADCN là hình gì ? Vì sao ? c/ Chứng minh M đối xứng với N qua A.d/ Tìm điều kiện của của ∆ABC để tứ giác AEDF là hình vuông?
Tứ giác AEDF là hình chữ nhật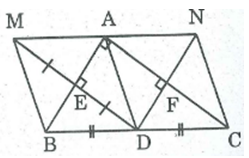
⇒ DE // AC; DF // AB
Trong ∆ ABC, ta có: DB = DC (gt)
Mà DE // AC
Suy ra: AE = EB (tính chất đường trung bình của tam giác)
Lại có: DF // AB và DB = DC
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM, ta có: AE = EB (cmt)
ED = EM (vì AB là trung trực DM)
Suy ra tứ giác ADBM là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Mặt khác: AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi (vì có hai đường chéo vuông góc)
Xét tứ giác ADCN, ta có: AF = FC (cmt)
DF = FN (vì AC là đường trung trực DN)
Suy ra tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
Lại có: AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo cắt nhau)

