Bài 2: Cho tam giác ABC, góc B góc C, AD là tia phân giáca) Chứng minh góc ADC - ADB góc B - Cb) Phân giác góc ngoài tại A của tam giác ABC cắt BC ở E. Chứng minh góc AEB 1/2 (B -C)Bài 3: Cho tam giác ABC, gọi D, E lần lượt là trung điểm của AC, AB. Trên tia đối của tia DB lấy M sao cho DM DB; trên tia đối của tia EC lấy N sao cho EN EC. Chứng minh A là trung điểm của MN?Bài 4: Cho tam giác ABC có góc A 50°. Vẽ đoạn thẳng AI vuông góc và bằng AB (I và C khác phía với AB). Vẽ đoạn thẳng AK...
Đọc tiếp
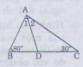
Bài 2: Cho tam giác ABC, góc B > góc C, AD là tia phân giác
a) Chứng minh góc ADC - ADB = góc B - C
b) Phân giác góc ngoài tại A của tam giác ABC cắt BC ở E. Chứng minh góc AEB = 1/2 (B -C)
Bài 3: Cho tam giác ABC, gọi D, E lần lượt là trung điểm của AC, AB. Trên tia đối của tia DB lấy M sao cho DM = DB; trên tia đối của tia EC lấy N sao cho EN = EC. Chứng minh A là trung điểm của MN?
Bài 4: Cho tam giác ABC có góc A = 50°. Vẽ đoạn thẳng AI vuông góc và bằng AB (I và C khác phía với AB). Vẽ đoạn thẳng AK vuong góc và bằng AC (K và B khác phía với AC). Chứng minh:
a) IC = BK
b) IC vuông góc BK
Bài 5: Cho tam giác ABC có góc A = 100°, M là trung điểm của BC, trên tia đối của MA lấy K sao cho MK = MA
a) Tính số đo góc ABK?
b) Ở phía ngoài tam giác ABC, vẽ AD vuông góc và bằng AB, AE vuông góc và bằng AC. Chứng minh hai tam giác ABK và DAE bằng nhau
c) Chứng minh MA vuông góc DE
Bài 6: Cho tam giác ABC có tia phân giác của góc ABC cắt cạnh AC ở D, tia phân giác của góc ACB cắt cạnh AB ở E. Biết BE + CD = BC. Tính số đo góc BAC?
Bài 7: Cho tam giác ABC có góc B = 2C. Tia phân giác của góc B cắt AC ở D. Trên tia đối của BD lấy E sao cho BE = AC. Trên tia đối của CB lấy K sao cho CK = AB. Chứng minh AE = AK.