Bài 1: Tính
a) \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
b) \(1\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
c) \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
d) \(\dfrac{2\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
Bài 2: Cho (d₁): y = \(\dfrac{1}{2}x-4\) và (d₂): y = \(-3x+3\) . Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm A của 2 đường thẳng trên.
Helpp!!
Bài 1:
a: \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
\(=5\cdot2\sqrt{2}-4\cdot3\sqrt{3}-2\cdot5\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-16\sqrt{3}\)
b: \(\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
\(=\left|3-\sqrt{6}\right|+\left|1-\sqrt{6}\right|\)
\(=3-\sqrt{6}+\sqrt{6}-1\)
=3-1=2
c: \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
\(=\dfrac{\sqrt{15}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{5}-\sqrt{3}}+\dfrac{1\left(4-\sqrt{15}\right)}{16-15}\)
\(=\sqrt{15}+4-\sqrt{15}=4\)
d: \(\dfrac{2\sqrt{3-\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
\(=\dfrac{\sqrt{3-\sqrt{5}}\cdot\sqrt{2}\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}\left(\sqrt{3}+1\right)}{2\left(\sqrt{3}+1\right)}\)
\(=\dfrac{\sqrt{6-2\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=\sqrt{\left(\sqrt{5}-1\right)^2}\cdot\dfrac{\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=3+\sqrt{5}-\dfrac{\sqrt{5}}{2}=3+\dfrac{\sqrt{5}}{2}\)
Bài 2:
Vẽ đồ thị:
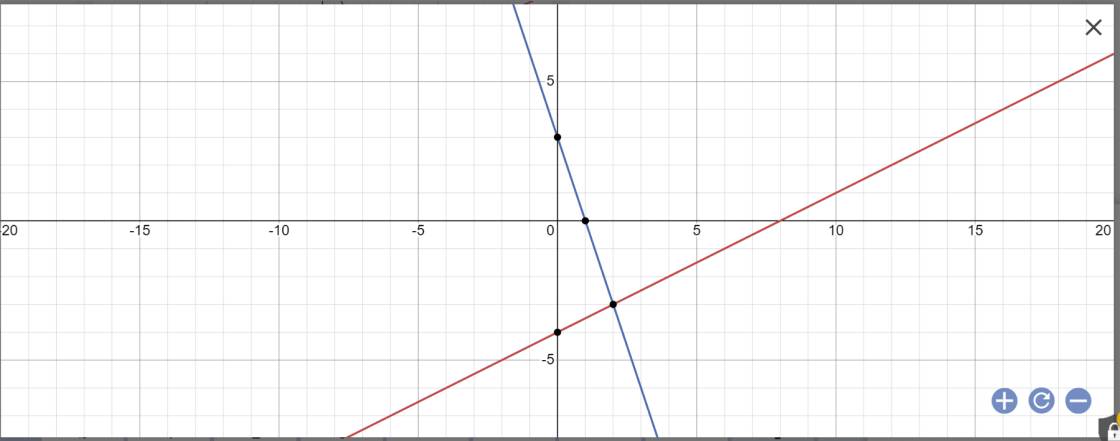
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x-4=-3x+3\)
=>\(\dfrac{1}{2}x+3x=3+4\)
=>\(\dfrac{7}{2}x=7\)
=>x=2
Thay x=2 vào y=-3x+3, ta được:
\(y=-3\cdot2+3=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)


