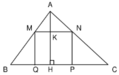
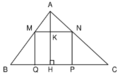
Bác Ba Phi có một mảnh vườn hình tam giác ABC với AB = 30m, AC = 40m và BC = 50m. Bác muốn đào một cái ao hình chữ nhật trên mảnh vườn này bằng cách chọn một điểm P trên cạnh BC rồi hạ các đường vuông góc PQ, PR lần lượt xuống AB, AC hình thành hình chữ nhật AQPR. Hỏi phải chọn điểm P cách B bao nhiêu mét để hình chữ nhật có diện tích lớn nhất? Diện tích lớn nhất đó bằng bao nhiêu mét vuông?
Pitago đảo \(\Rightarrow\Delta ABC\) vuông tại A
Ta có: \(PQ||AC\) (cùng vuông góc AB)
\(\Rightarrow\dfrac{PQ}{AC}=\dfrac{BP}{BC}\)
Tương tự: \(\dfrac{PR}{AB}=\dfrac{CP}{BC}\)
\(\Rightarrow\dfrac{PQ.PR}{AB.AC}=\dfrac{BP.CP}{BC^2}\)
\(\Rightarrow PQ.PR=\dfrac{30.40}{50^2}.BP.CP=\dfrac{12}{25}BP.CP\le\dfrac{3}{25}\left(BP+CP\right)^2=\dfrac{3}{25}.BC^2=300\)
Dấu "=" xảy ra khi \(BP=CP\) hay P là trung điểm BC
P cách B 25m