Lời giải:
ĐKXĐ: $x\neq \pm 3; x\neq 0$
a. \(A=\left[\frac{-(x-3)}{x+3}.\frac{(x+3)^2}{(x-3)(x+3)}+\frac{x}{x+3}\right].\frac{x+3}{3x^2}\)
\(=\left(-1+\frac{x}{x+3}\right).\frac{x+3}{3x^2}=\frac{-3}{x+3}.\frac{x+3}{3x^2}=\frac{-1}{x^2}\)
b. Với $x=\frac{-1}{2}$ thì $x^2=\frac{1}{4}$
$\Rightarrow A=\frac{-1}{\frac{1}{4}}=-4$
c.
Với $x\neq 0, \pm 3$ thì $\frac{1}{x^2}>0\Leftrightarrow A=\frac{-1}{x^2}< 0$ với mọi $x\neq 0; x\neq \pm 3$
a) Ta có: \(A=\left(\dfrac{3-x}{x+3}\cdot\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-\left(x-3\right)}{x+3}\cdot\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
\(=\left(\dfrac{-x-3+x}{x+3}\right)\cdot\dfrac{x+3}{3x^2}\)
\(=-\dfrac{1}{x^2}\)
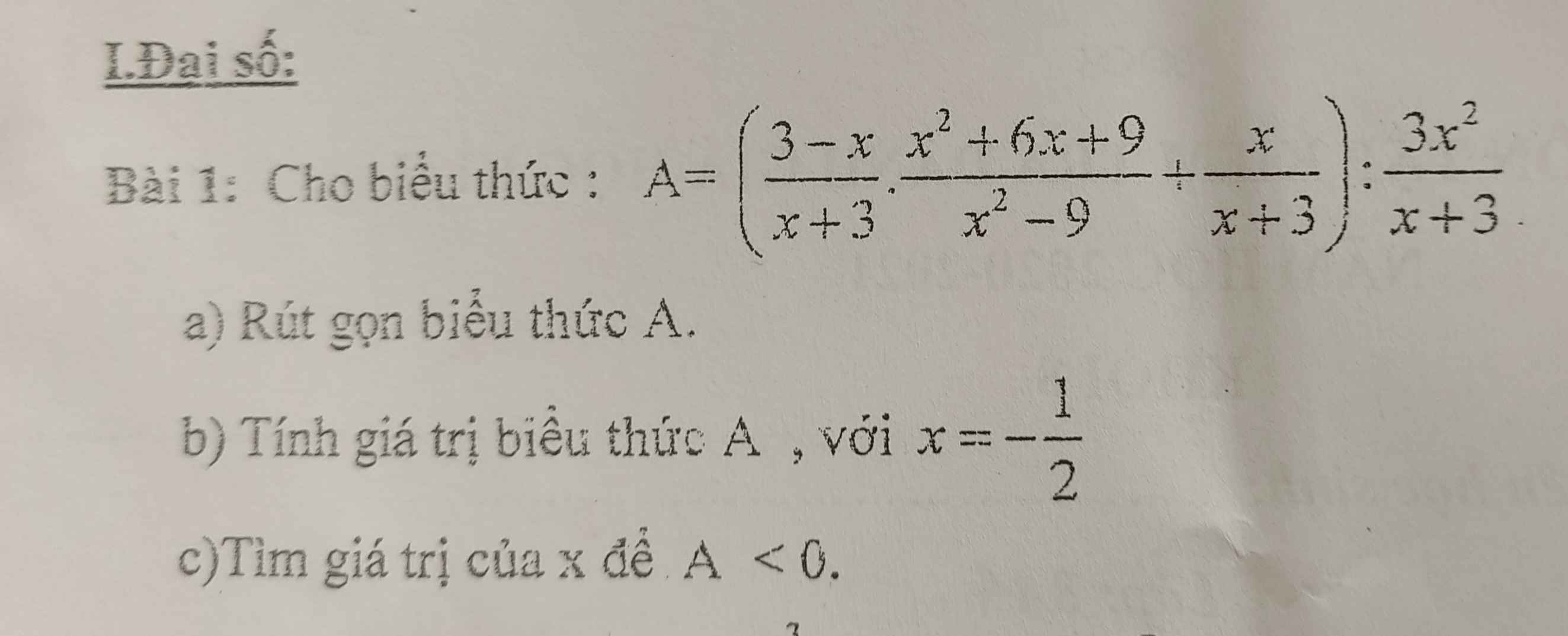




 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ