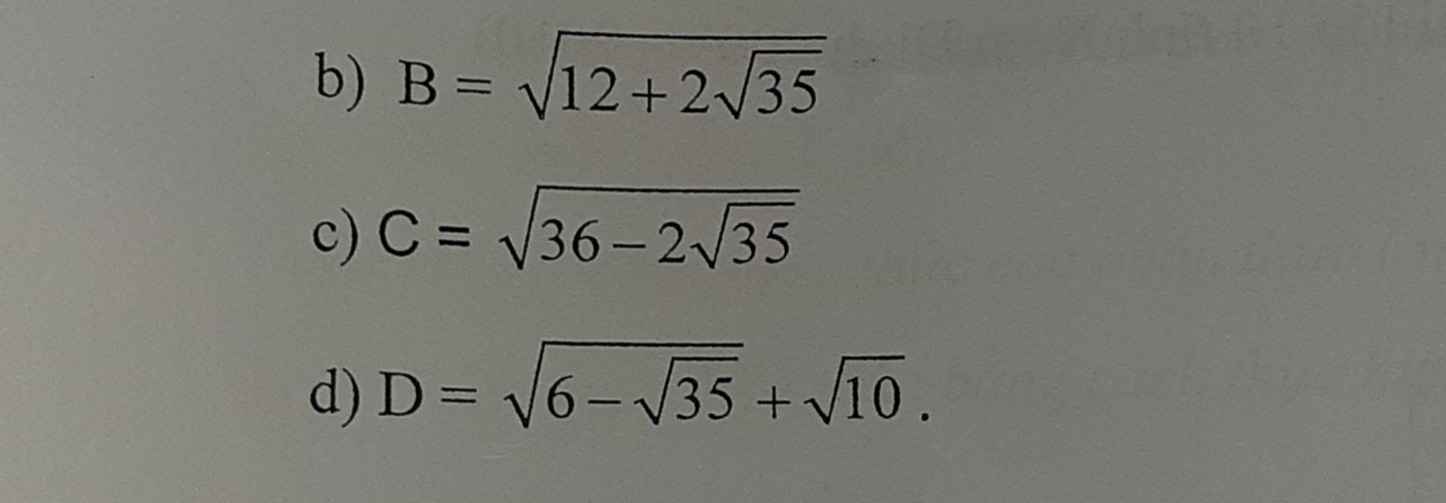b) \(B=\sqrt{12+2\sqrt{35}}=\sqrt{12+2.\sqrt{7}.\sqrt{5}}=\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.\sqrt{5}+\left(\sqrt{5}\right)^2}=\sqrt{\left(\sqrt{7}+\sqrt{5}\right)^2}=\left|\sqrt{7}+\sqrt{5}\right|\)
Vì \(\sqrt{7}>\sqrt{5}\) nên \(\left|\sqrt{7}+\sqrt{5}\right|=\sqrt{7}+\sqrt{5}\)
d) \(D=\sqrt{6-\sqrt{35}}+\sqrt{10}=\sqrt{2}.\sqrt{6-\sqrt{35}}+\sqrt{5}=\sqrt{12-\sqrt{35}}+\sqrt{5}=\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}+\sqrt{5}=\left|\sqrt{7}-\sqrt{5}\right|+\sqrt{5}=\sqrt{7}-\sqrt{5}+\sqrt{5}=\sqrt{7}\)