b: Để hai đường thẳng y=mx+1 và y=(3-2m)x-3 song song thì
\(\left\{{}\begin{matrix}m=3-2m\\1\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m=3-2m
=>3m=3
=>m=1
a: 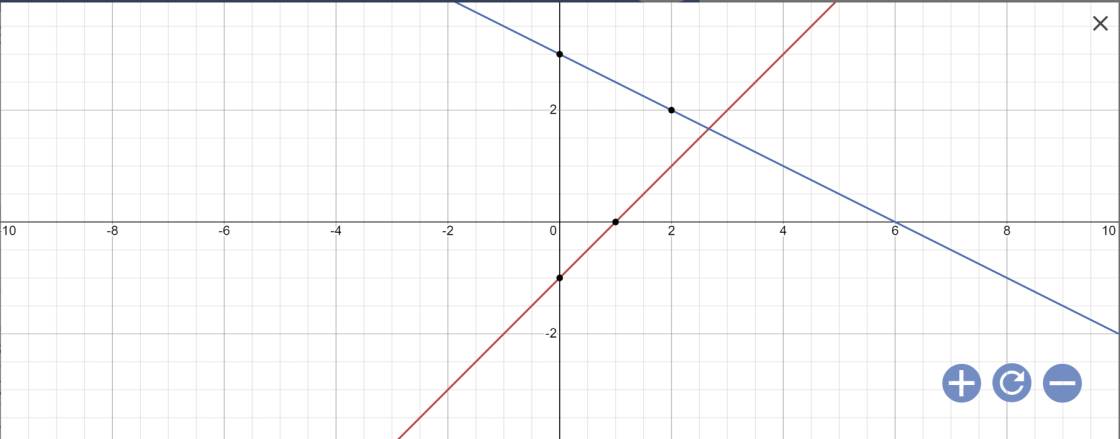
TK:
a) Để vẽ đồ thị của hai hàm số \(d_1\) và \(d_2\), chúng ta cần biểu diễn chúng dưới dạng phương trình hình học y = mx + c.
- Hàm số \(d_1\) có phương trình y = x - 1, nên ta có \(m_1 = 1\) và \(c_1 = -1\).
- Hàm số \(d_2\) có phương trình y = -1/2 * x + 3, nên ta có \(m_2 = -1/2\) và \(c_2 = 3\).
Sau đó, chúng ta vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ.
b) Để hai đồ thị là hai đường thẳng song song với nhau, hệ số góc của hai đường thẳng cần phải bằng nhau. Tức là \(m_1 = m_2\).
Ta có hàm số \(y = mx + 1\), với \(m = 1\) thì có \(y = x + 1\).
Và ta có hàm số \(y = (3 - 2m) \times x - 3\), với \(m = 1\) thì có \(y = (3 - 2 \times 1) \times x - 3 = 1 \times x - 3\).
Do đó, với \(m = 1\), đồ thị của hai hàm số là hai đường thẳng song song với nhau.



