Lời giải:
$4x-y+2xy=14$
$(4x+2xy)-y=14$
$2x(2+y)-(y+2)=12$
$(y+2)(2x-1)=12$
Do $y$ là số tự nhiên nên $y+2$ là số tự nhiên.
$(y+2)(2x-1)=12>0, y+2>0$ nên $2x-1>0$
Vậy $y+2, 2x-1$ là số tự nhiên có tích là 12. $2x-1$ lẻ nên ta có các TH sau:
TH1: $2x-1=1, y+2=12$
$\Rightarrow x=1; y=10$
TH2: $2x-1=3, y+2=4$
$\Rightarrow x=2; y=2$
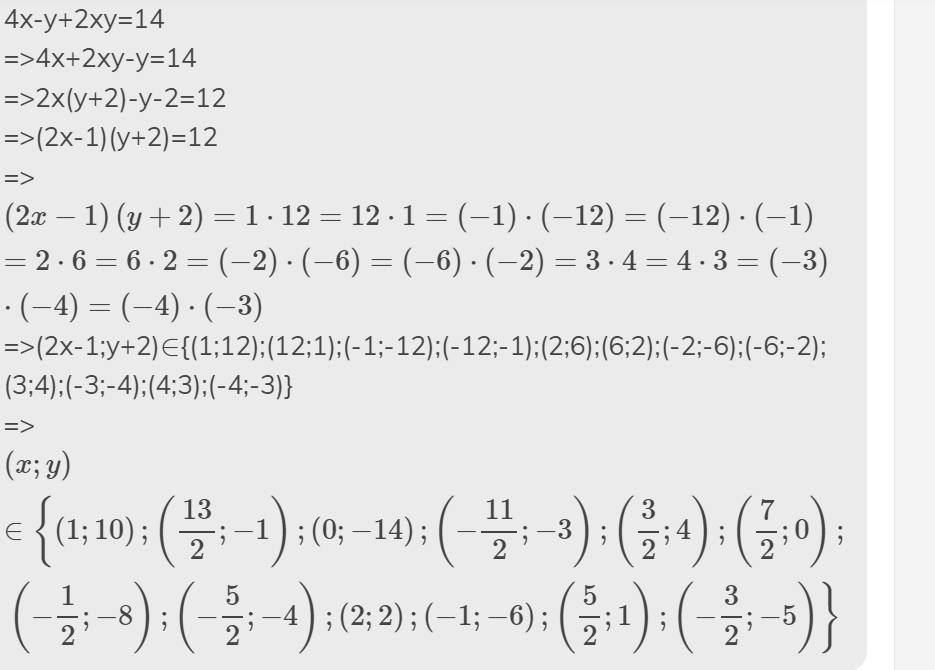
mà (x;y) là các số tự nhiên
nên \(\left(x;y\right)\in\left\{\left(1;10\right);\left(2;2\right)\right\}\)


