Đầu tiên ta luôn luôn đưa hệ số của bình phương về 1 bằng cách đặt nhân tử chung:
\(2m^2-3m+1=2\left(m^2-\dfrac{3}{2}m+\dfrac{1}{2}\right)\)
Sau đó là tận dụng hằng đẳng thức: \(\left(a-b\right)^2=a^2-2ab...\) , ở đây vai trò của a là m và vai trò của 2ab là \(-\dfrac{3}{2}m\)
Nghĩa là ta phải tách \(\dfrac{3}{2}m\) về dạng 2ab với a là m, hay nó là: \(2.m.b\)
\(\Rightarrow-\dfrac{3}{2}m=2mb\)
\(\Rightarrow b=\left(\dfrac{3}{2}m\right):\left(2m\right)=\dfrac{3}{4}\)
\(\Rightarrow b^2=\dfrac{9}{16}\)
Vậy ta cần thêm bớt 9/16 vào
\(2\left(m^2-\dfrac{3}{2}m+\dfrac{1}{2}\right)=2\left(m^2-\dfrac{3}{2}m+\dfrac{9}{16}-\dfrac{9}{16}+\dfrac{1}{2}\right)\)
\(=2\left(m^2-2.m.\dfrac{3}{2}+\dfrac{9}{16}-\dfrac{1}{16}\right)=2\left[\left(m-\dfrac{3}{2}\right)^2-\dfrac{1}{16}\right]\)
\(=2\left(m-\dfrac{3}{2}\right)^2-\dfrac{1}{8}\)
Cách sử dụng máy tính cầm tay:
Ví dụ cần tách đa thức bậc 2 dạng \(ax^2+bx+c\)
Đa thức này luôn tách được về dạng:
\(a\left(x-X_{max-min}\right)^2+Y_{max-min}\) (1)
Cách làm:
Nhập giải pt bậc 2 (tùy dòng máy, ví dụ FX 570 là Mode 5-3)
Nhập các hệ số, sau đó nhấn = liên tục, đến khi thấy nó hiện:
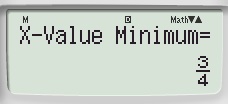
Vậy \(X_{min}=\dfrac{3}{4}\) (nếu hệ số a âm sẽ ra Xmax, hệ số a dương ra Xmin)
Bấm tiếp dấu =, nó ra:
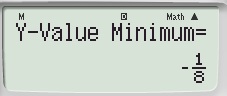
Vậy \(Y_{min}=-\dfrac{1}{8}\)
Thay vào (1) ta được:
\(2m^2-3m+1=2\left(m-\dfrac{3}{4}\right)^2-\dfrac{1}{8}\)
Mất 3s mà ko cần nghĩ cách tách mệt đầu :D
Biến thành hằng đẳng thức là sao em? Phân tích thành nhân tử hay tách bình phương?
\(2m^2-3m+1=\left(m-1\right)\left(2m-1\right)\)
Hay em muốn tách kiểu này:
\(2m^2-3m+1=2\left(m-\dfrac{3}{4}\right)^2-\dfrac{1}{8}\)



