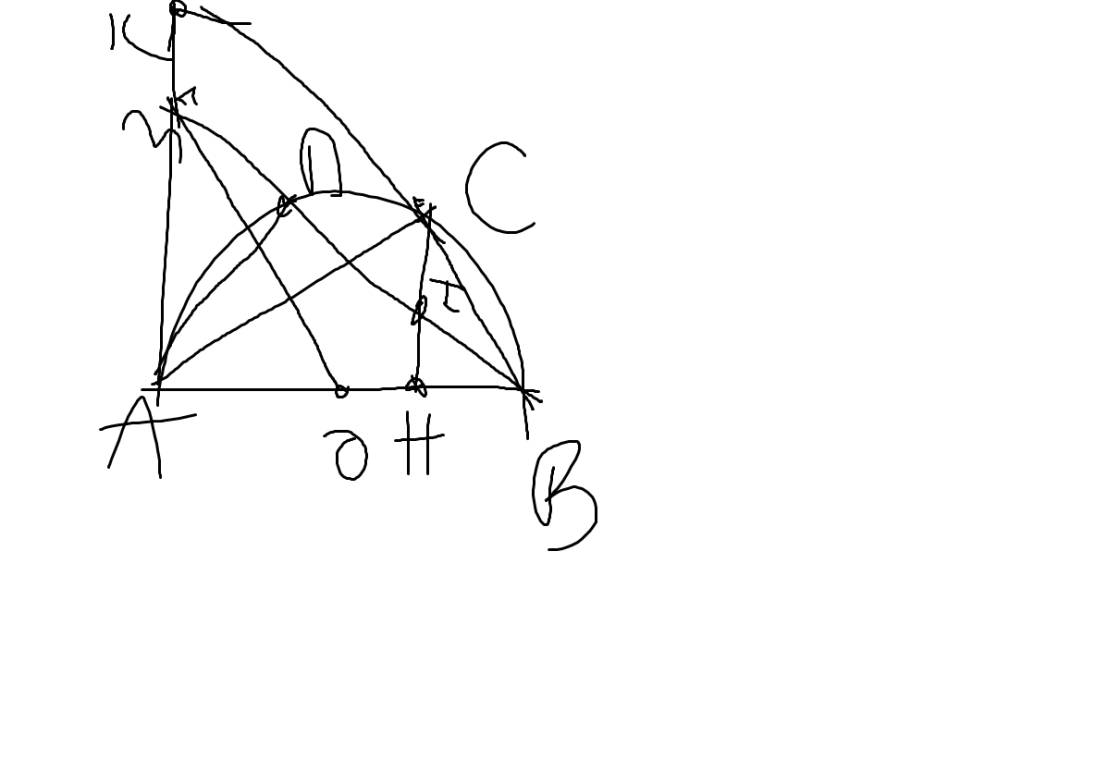
1/.Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). MB cắt nửa đường tròn (O) tại D (D khác B).
a) Chứng minh tứ giác AMCO nội tiếp.
b) Chứng minh MC2=MD.MB
c) Vẽ CH vuông góc với AB (H thuộc AB). Chứng minh MB đi qua trung điểm của CH
Vẽ Hình Nx Ah.
a: Xét tứ giác AMCO có \(\widehat{MAO}+\widehat{MCO}=90^0+90^0=180^0\)
nên AMCO là tứ giác nội tiếp
b: Xét (O) có
MA,MC là các tiếp tuyến
Do đó: MA=MC
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)MB tại D
Xét ΔMAB vuông tại A có AD là đường cao
nên \(MD\cdot MB=MA^2\)
=>\(MD\cdot MB=MC^2\)
c: Gọi giao điểm của CH với MB là I, giao điểm của CB với AM là K
Ta có: CH\(\perp\)AB
AM\(\perp\)AB
Do đó: CH//AM
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)KB tại C
Ta có: \(\widehat{MKC}+\widehat{MAC}=90^0\)(ΔKCA vuông tại C)
\(\widehat{MCK}+\widehat{MCA}=\widehat{KCA}=90^0\)
mà \(\widehat{MAC}=\widehat{MCA}\)(MA=MC)
nên \(\widehat{MKC}=\widehat{MCK}\)
=>MC=MK
mà MC=MA
nên MA=MK(1)
Xét ΔBMA có IH//MA
nên \(\dfrac{IH}{MA}=\dfrac{BI}{BM}\left(2\right)\)
Xét ΔBMK có CI//MK
nên \(\dfrac{CI}{MK}=\dfrac{BI}{BM}\left(3\right)\)
Từ (1),(2),(3) suy ra CI=IH
=>I là trung điểm của CH(ĐPCM)