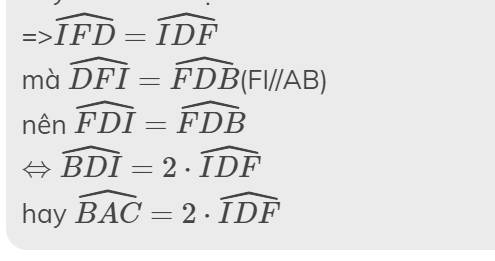1.Cho △ABC có AB>AC.Trên cạnh AB lấy điểm E sao cho BE=AC.Gọi I,D,F theo thứ tự là trung điểm của CE,AE,BC.C/m
a.△IDF là tam giác cân
b.Góc BAC =2.IDF
2.Cho △ABC trung tuyến AM.Đường phân giác của góc AMB cắt cạnh AB tại D,đường phân giác của góc AMC cắt cạnh AC tại E.
a.c/m DE//BC
b.Gọi I là giao điểm của DE và AM.C/m I là trung điểm của DE
Bài 2:
a: Xét ΔMAB có MD là phân giác
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}=\dfrac{AM}{MC}\left(1\right)\)
Xét ΔMAC có ME là phân giác
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
Xét ΔABC có \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
b: Xét ΔABM có DI//BM
nên \(\dfrac{DI}{BM}=\dfrac{AI}{AM}\left(3\right)\)
Xét ΔAMC có IE//MC
nên \(\dfrac{IE}{MC}=\dfrac{AI}{AM}\left(4\right)\)
Từ (3),(4) suy ra \(\dfrac{DI}{BM}=\dfrac{IE}{MC}\)
mà BM=MC
nên DI=IE
=>I là trung điểm của DE
Bài 1:
a: XétΔAEC có
D,I lần lượt là trung điểm của EA,EC
=>DI là đường trung bình của ΔAEC
=>DI//AC và DI=AC/2
Xét ΔECB có
I,F lần lượt là trung điểm của CE,CB
=>IF là đường trung bình của ΔECB
=>IF//EB và IF=EB/2
Ta có: \(ID=\dfrac{AC}{2}\)
\(IF=\dfrac{EB}{2}\)
mà AC=EB
nên ID=IF
=>ΔIDF cân tại I
b: Ta có: ΔIDF cân tại I