1, Giả sử a,b,c là các số thực khác 0 thỏa mãn (a+b)(b+c)(c+a)=8abc
CMR: \(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}=\dfrac{3}{4}+\dfrac{ab}{\left(a+b\right)\left(b+c\right)}+\dfrac{bc}{\left(b+c\right)\left(c+a\right)}+\dfrac{ca}{\left(c+a\right)\left(a+b\right)}\)
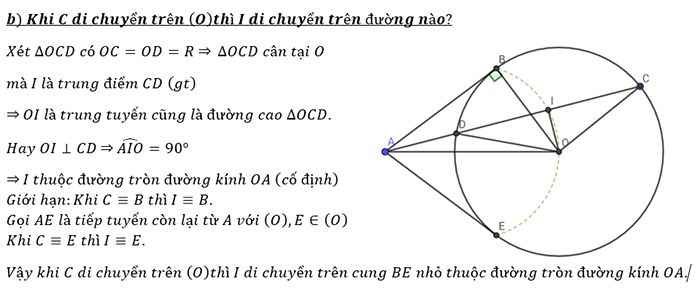
2,Cho đường tròn tâm O bán kính R=6cm và 1 điểm A cách O 1 khoảng 10cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm). Vẽ cát tuyến ACD, gọi I là trung điểm của đoạn CD. Hỏi khi chạy trên đường tròn thì I chạy trên đường nào?
1.
Đặt \(\left(x;y;z\right)=\left(\dfrac{a}{a+b};\dfrac{b}{b+c};\dfrac{c}{c+a}\right)\Rightarrow\left\{{}\begin{matrix}1-x=\dfrac{b}{b+a}\\1-y=\dfrac{c}{b+c}\\1-z=\dfrac{a}{a+c}\end{matrix}\right.\)
\(\Rightarrow xyz=\dfrac{1}{8}\\ xyz=\left(1-x\right)\left(1-y\right)\left(1-z\right)\\ \Rightarrow xyz=1-\left(x+y+z\right)+\left(xy+yz+zx\right)-xyz\\ \Rightarrow2xyz=1-\left(x+y+z\right)+\left(xy+yz+zx\right)=\dfrac{1}{4}\\ \Rightarrow x+y+z=\dfrac{3}{4}+xy+yz+zx\)
\(\RightarrowĐpcm\)