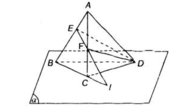
1. Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D,E là các điểm lần lượt thuộc các cạnh SA, SB và D,E khác S a. Đường thẳng DE có nằm trong mặt phẳng (SAB) không? b. Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE) 2. Cho hình chóp tứ giác S. ABCD và M là một điểm thuộc cạnh SC ( M khác S,C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD)
1:
a: \(D\in SA\subset\left(SAB\right);E\in SB\subset\left(SAB\right)\)
Do đó: \(DE\subset\left(SAB\right)\)
b: \(F\in AB\subset\left(SAB\right)\)
\(F\in DE\subset\left(CDE\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(CDE\right)\)
2:
\(N\in AB\subset\left(ABM\right);N\in CD\subset\left(SCD\right)\)
Do đó: \(N\in\left(ABM\right)\cap\left(SCD\right)\)
\(M\in SC\subset\left(SCD\right);M\in MB\subset\left(ABM\right)\)
Do đó: \(M\in\left(ABM\right)\cap\left(SCD\right)\)
Do đó: \(\left(ABM\right)\cap\left(SCD\right)=MN\)