1. Cho hình vuông ABCD. M là 1 điểm thay đổi trên cạnh BC, M không trùng với B và C. Qua A kẻ tia Ax vuông góc với AM, Ax cắt CD tại N, đường trung tuyến AI của tam giác AMN cắt CD ở K. Đường thẳng qua M song song với AB cắt AI ở G.
Chứng minh rằng:
a) Tứ giác MGNK là hình thoi;
b) AN2=NK.NC;
c) Chu vi tam giác MKC không đổi;
d) 3 điểm B,I,D thẳng hàng.
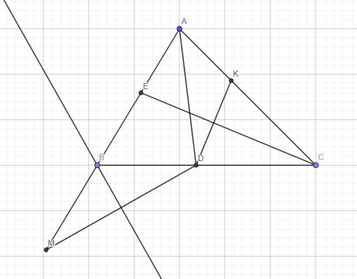
2. Cho hình thoi ABCD cạnh a, có A=60o. Một đường thẳng bất kỳ đi qua C cắt tia đối của các tia BA, DA tương ứng ở M, N.
a) Chứng minh: BM.DN=a2
b) Gọi K là giao điểm của BN và DM. Tính góc BKD.
3. Cho tam giác ABC, phân giác AD, CE. Trên AC lấy điểm K sao cho KD⊥CE. Trên AB lấy điểm M sao cho MD vuông góc với phân giác ngoài góc B. Tính AK biết AM=16, AD=8.
Theo cách dựng ta có CE vừa là đường cao, vừa là phân giác trong tam giác CDK
\(\Rightarrow\Delta CDK\) cân tại C
\(\Rightarrow DC=CK\)
Tương tự ta có: \(BM=DB\)
Mặt khác theo định lý phân giác: \(\dfrac{AB}{AC}=\dfrac{DB}{DC}\Rightarrow AB.DC=AC.DB\)
\(\Rightarrow AB.DC-AC.DB=0\)
Dễ dàng chứng minh bài toán quen thuộc: \(AD^2=AB.AC-BD.DC\)
\(\Rightarrow AD^2=\left(AM-DB\right)\left(AK+DC\right)-DB.DC\)
\(=AM.AK+AM.DC-DB.AK-DB.DC-DB.DC\)
\(=AM.AK+DC\left(AM-DB\right)-DB\left(AK+DC\right)\)
\(=AM.AK+DC.AB-DB.AC\)
\(=AM.AK\)
\(\Rightarrow AK=\dfrac{AD^2}{AM}=4\)