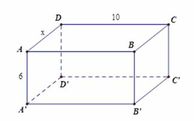
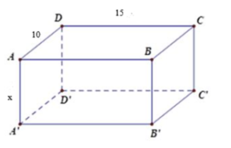
Diện tích đáy của thùng là:
\(\dfrac{2x^3+3x^2-8x+3}{x-1}\left(cm^2\right)\)
Chiều rộng hình hộp chữ nhật bằng:
\(\left(2x^3+3x^2-8x+3\right):\left(x+3\right)\left(x-1\right)\)
\(=\left(2x^3+6x^2-3x^2-9x+x+3\right):\left(x+3\right)\left(x-1\right)\)
\(=\left[2x^2\left(x+3\right)-3x\left(x+3\right)+\left(x+3\right)\right]:\left(x+3\right)\left(x-1\right)\)
\(=\left[\left(x+3\right)\left(2x^2-3x+1\right)\right]:\left(x+3\right)\left(x-1\right)\)
\(=\dfrac{\left(x+3\right)\left(2x^2-2x-x+1\right)}{\left(x+3\right)\left(x-1\right)}\)
\(=\dfrac{2x\left(x-1\right)-\left(x-1\right)}{x-1}\)
\(=\dfrac{\left(x-1\right)\left(2x-1\right)}{x-1}\)
\(=2x-1\left(cm\right)\)
Khi đó, diện tích đáy hình hộp chữ nhật bằng:
\(\left(x+3\right)\left(2x-1\right)=2x^2+5x-3\left(cm\right)\)
#\(Toru\)
\(V=a.b.h\Rightarrow a.b=\dfrac{V}{h}\)
\(\Rightarrow a.b=\dfrac{V}{h}=\dfrac{2x^3+3x^2-8x+3}{x-1}=2x^2+5x-3\left(cm^2\right)\)
Đáp số...