Câu 1
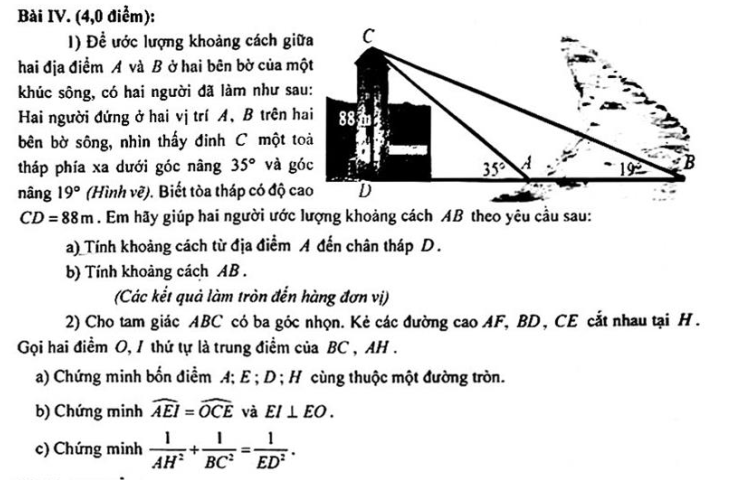
a) Xét \(\Delta ACD:tan35^o=\dfrac{CD}{AD}\Leftrightarrow AD=\dfrac{CD}{tan35^o}=\dfrac{88.}{tan35^o}\approx126\left(m\right)\)
b) Xét \(\Delta BCD:tan19^o=\dfrac{CD}{BD}\Leftrightarrow BD=\dfrac{CD}{tan19^o}=\dfrac{88.}{tan19^o}\approx256\left(m\right)\)
\(AB=BD-AD=256-126=130\left(m\right)\)
Câu 2:
a: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
nên ADHE là tứ giác nội tiếp đường tròn đường kính AH
=>A,D,H,E cùng thuộc một đường tròn
b: ΔAEH vuông tại E
mà EI là đường trung tuyến
nên IE=IA
=>ΔIAE cân tại I
=>\(\widehat{AEI}=\widehat{IAE}=\widehat{FAB}\)
mà \(\widehat{FAB}=\widehat{OCE}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{AEI}=\widehat{OCE}\)
ΔEBC vuông tại E
mà EO là đường trung tuyến
nên OE=OC=OB
OE=OC nên ΔOEC cân tại O
=>\(\widehat{OEC}=\widehat{OCE}\)
\(\widehat{IEO}=\widehat{IEC}+\widehat{OEC}=\widehat{IEC}+\widehat{OCE}=\widehat{IEC}+\widehat{AEI}=90^0\)
=>EI\(\perp\)EO
c: ΔADH vuông tại D
mà DI là đường trung tuyến
nên ID=IH
mà IH=IE
nên ID=IE
=>I nằm trên đường trung trực của DE(1)
Ta có: ΔDBC vuông tại D
mà DO là đường trung tuyến
nên DO=OB
mà OB=OE
nên OE=OD
=>O nằm trên đường trung trực của DE(2)
Gọi K là giao điểm của OI và DE
Từ (1),(2) suy ra OI là đường trung trực của DE
=>OI\(\perp\)DE tại K và K là trung điểm của DE
Xét ΔIEO và ΔIDO có
IE=ID
EO=DO
IO chung
Do đó: ΔIEO=ΔIDO
=>\(\widehat{IEO}=\widehat{IDO}=90^0\)
Xét ΔIDO vuông tại D có DK là đường cao
nên \(\dfrac{1}{DK^2}=\dfrac{1}{DI^2}+\dfrac{1}{DO^2}\)
=>\(\dfrac{1}{4\cdot DK^2}=\dfrac{1}{DI^2\cdot4}+\dfrac{1}{4\cdot DO^2}\)
=>\(\dfrac{1}{\left(2DK\right)^2}=\dfrac{1}{\left(2DO\right)^2}+\dfrac{1}{\left(2DI\right)^2}\)
=>\(\dfrac{1}{AH^2}+\dfrac{1}{BC^2}=\dfrac{1}{ED^2}\)