Bài 1
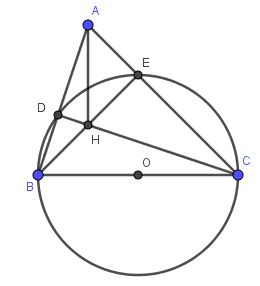
a) Do (O) đường kính BC cắt AB tại D và cắt AC tại E
\(\Rightarrow D,E\) cùng thuộc (O)
\(\Rightarrow\widehat{BDC}=\widehat{BEC}=90^0\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{BDC}=90^0\)
b) Do \(\widehat{BDC}=90^0\left(cmt\right)\)
\(\Rightarrow CD\perp AB\)
Do \(\widehat{BEC}=90^0\left(cmt\right)\)
\(\Rightarrow BE\perp AC\)
\(\Delta ABC\) có:
\(CD\perp AB\left(cmt\right)\)
\(\Rightarrow CD\) là đường cao của \(\Delta ABC\left(1\right)\)
\(BE\perp AC\left(cmt\right)\)
\(\Rightarrow BE\) là đường cao thứ hai của \(\Delta ABC\left(2\right)\)
Lại có H là giao điểm của BE và CD (gt) (3)
Từ (1), (2) và (3) \(\Rightarrow AH\) là đường cao thứ ba của \(\Delta ABC\)
\(\Rightarrow AH\perp BC\)
Bài 2
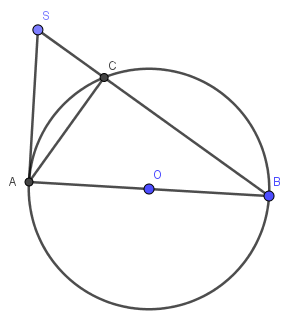
Do SB cắt (O) tại C
\(\Rightarrow\) \(C\in\left(O\right)\)
\(\Rightarrow\widehat{ACB}=90^0\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{ACS}=180^0-\widehat{ACB}=180^0-90^0=90^0\)
\(\Rightarrow\Delta ACS\) vuông tại C
Do SA là tiếp tuyến của (O) (gt)
\(\Rightarrow\widehat{SAB}=90^0\)
\(\Rightarrow\Delta BAS\) vuông tại A
Xét hai tam giác vuông: \(\Delta ACS\) và \(\Delta BAS\) có:
\(\widehat{S}\) chung
\(\Rightarrow\Delta ACS\sim\Delta BAS\left(g-g\right)\)
\(\Rightarrow\dfrac{SA}{SB}=\dfrac{SC}{SA}\)
\(\Rightarrow SA^2=SB.SC\)
Bài 3
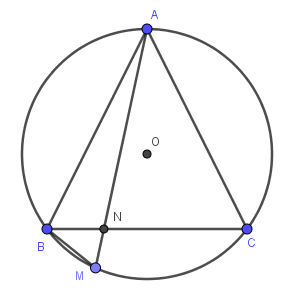
Do \(\Delta ABC\) cân tại A
\(\Rightarrow AB=AC\)
\(\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}\)
\(\Rightarrow\widehat{AMB}=\widehat{ABC}\) (hai góc nội tiếp chắn hai cung bằng nhau)
\(\Rightarrow\widehat{AMB}=\widehat{ABN}\)
Xét \(\Delta AMB\) và \(\Delta ABN\) có:
\(\widehat{A}\) chung
\(\widehat{AMB}=\widehat{ABN}\) (cmt)
\(\Rightarrow\Delta AMB\sim\Delta ABN\left(g-g\right)\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AB}{AN}\)
\(\Rightarrow AM.AN=AB^2\)


