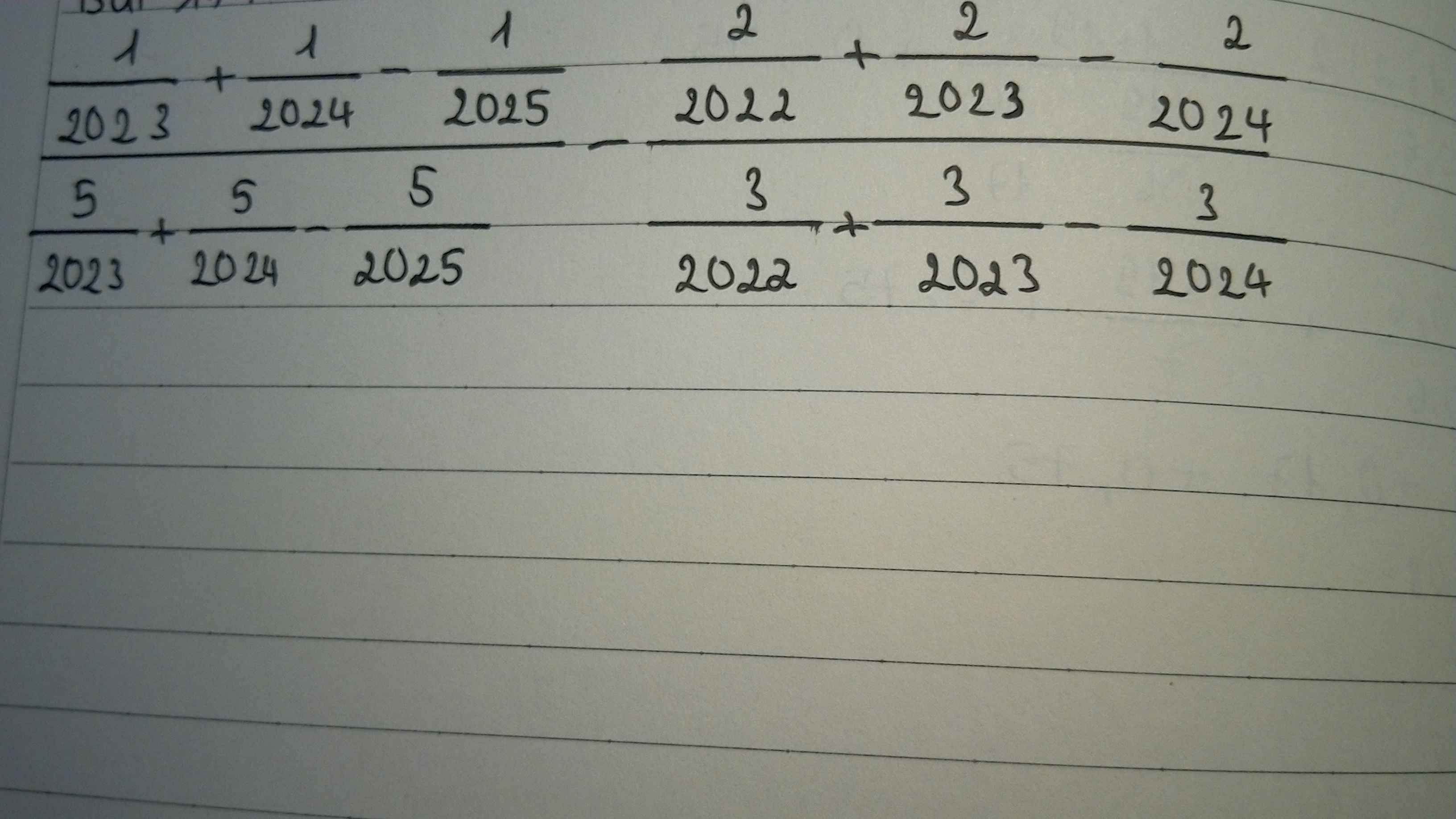Ta có: \(\dfrac{\dfrac{1}{2023}+\dfrac{1}{2024}-\dfrac{1}{2025}}{\dfrac{5}{2023}+\dfrac{5}{2024}-\dfrac{5}{2025}}-\dfrac{\dfrac{2}{2022}+\dfrac{2}{2023}-\dfrac{2}{2024}}{\dfrac{3}{2022}+\dfrac{3}{2023}-\dfrac{3}{2024}}\)
\(=\dfrac{\dfrac{1}{2023}+\dfrac{1}{2024}-\dfrac{1}{2025}}{5\left(\dfrac{1}{2023}+\dfrac{1}{2024}-\dfrac{1}{2025}\right)}-\dfrac{2\left(\dfrac{1}{2022}+\dfrac{1}{2023}-\dfrac{1}{2024}\right)}{3\left(\dfrac{1}{2022}+\dfrac{1}{2023}-\dfrac{1}{2024}\right)}\)
\(=\dfrac{1}{5}-\dfrac{2}{3}\)
\(=\dfrac{3}{15}-\dfrac{10}{15}=-\dfrac{7}{15}\)
Đúng 2
Bình luận (0)