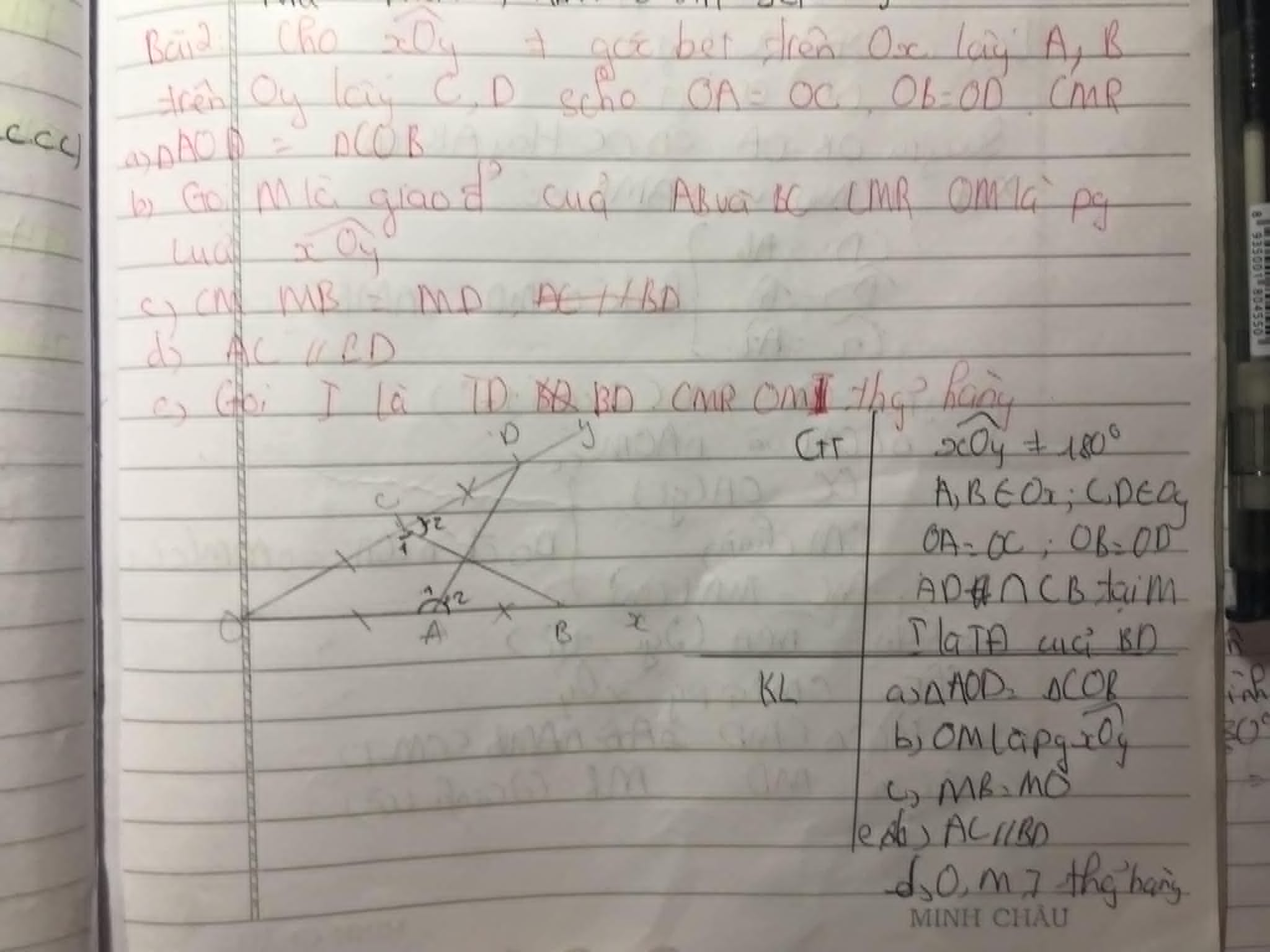
a: Xét ΔOAD và ΔOCB có
OA=OC
\(\widehat{AOD}\) chung
OD=OB
Do đó: ΔOAD=ΔOCB
b: ΔOAD=ΔOCB
=>\(\widehat{ODA}=\widehat{OBC}\)
ΔOAD=ΔOCB
=>\(\widehat{OAD}=\widehat{OCB}\)
mà \(\widehat{OAD}+\widehat{BAD}=180^0\)(hai góc kề bù)
và \(\widehat{OCB}+\widehat{DCB}=180^0\)(hai góc kề bù)
nên \(\widehat{BAD}=\widehat{DCB}\)
Ta có: OA+AB=OB
OC+CD=OD
mà OA=OC và OB=OD
nên AB=CD
Xét ΔMAB và ΔMCD có
\(\widehat{MAB}=\widehat{MCD}\)
AB=CD
\(\widehat{MBA}=\widehat{MDC}\)
Do đó: ΔMAB=ΔMCD
=>MA=MC
Xét ΔOAM và ΔOCM có
OA=OC
AM=CM
OM chung
Do đó: ΔOAM=ΔOCM
=>\(\widehat{AOM}=\widehat{COM}\)
=>OM là phân giác của góc AOC
=>OM là phân giác của góc xOy
c: ΔMAB=ΔMCD
=>MB=MD
d: Xét ΔOBD có \(\dfrac{OA}{AB}=\dfrac{OC}{CD}\)
nên AC//BD
e: Ta có: IB=ID
=>I nằm trên đường trung trực của BD(1)
Ta có: MB=MD
=>M nằm trên đường trung trực của BD(2)
Ta có: OD=OB
=>O nằm trên đường trung trực của BD(3)
Từ (1),(2),(3) suy ra O,M,I thẳng hàng