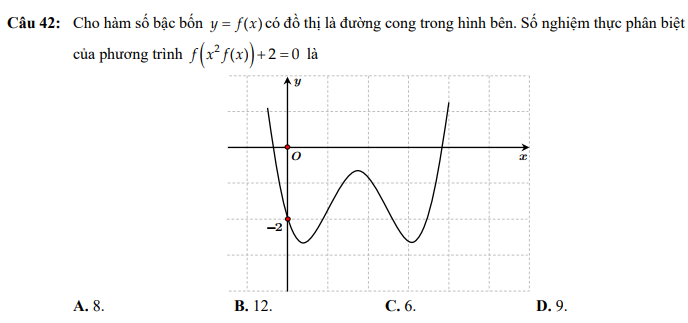
\(f\left(x^2.f\left(x\right)\right)=-2\Rightarrow\left[{}\begin{matrix}x^2.f\left(x\right)=0\\x^2.f\left(x\right)=a;b;c\\\end{matrix}\right.\)
Với \(0< a< b< c\)
Phương trình \(x^2.f\left(x\right)=0\) có 3 nghiệm
Xét \(f\left(x\right)=\dfrac{a}{x^2}\) với \(a>0\)
Đồ thị \(\dfrac{a}{x^2}\) (dễ dàng lập BBT) có 2 nhánh nằm 2 bên trục Oy, nên mỗi nhánh cắt f(x) tại 1 điểm
Do đó \(f\left(x\right)=\dfrac{a}{x^2}\) luôn có 2 nghiệm với mọi a dương
\(\Rightarrow\)Có \(3+3.2=9\) nghiệm
Đúng 2
Bình luận (0)