\(g\left(x\right)=f\left(1-\dfrac{1}{x^2}\right)+\dfrac{2}{x}\)
Đặt \(u=\dfrac{1}{x}\)
\(g\left(u\right)=g\left(\dfrac{1}{x}\right)=f\left(1-u^2\right)+2u\)
\(g'\left(u\right)=-2u'.\left[u.f'\left(1-u^2\right)-1\right]=0\)
\(\Rightarrow f'\left(1-u^2\right)=\dfrac{1}{u}\) (1)
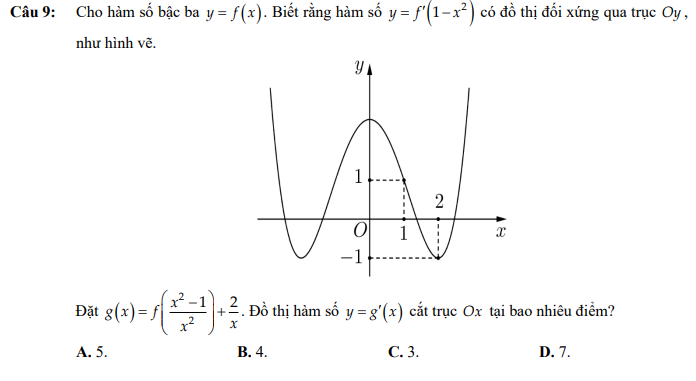
Vẽ lên cùng hệ trục đồ thị \(y=\dfrac{1}{u}\Rightarrow\left(1\right)\) có 3 nghiệm: \(\left[{}\begin{matrix}u=a\in\left(0;1\right)\\u=1\\u=b>2\end{matrix}\right.\)
Ứng với mỗi giá trị u có đúng 1 giá trị x tương ứng
Nên C đúng
Đúng 1
Bình luận (0)