a: Thay x=1 và y=-1 vào \(y=ax^2\), ta được:
\(a\cdot1^2=-1\)
=>a*1=-1
=>a=-1
=>\(y=-x^2\)
Vẽ đồ thị:
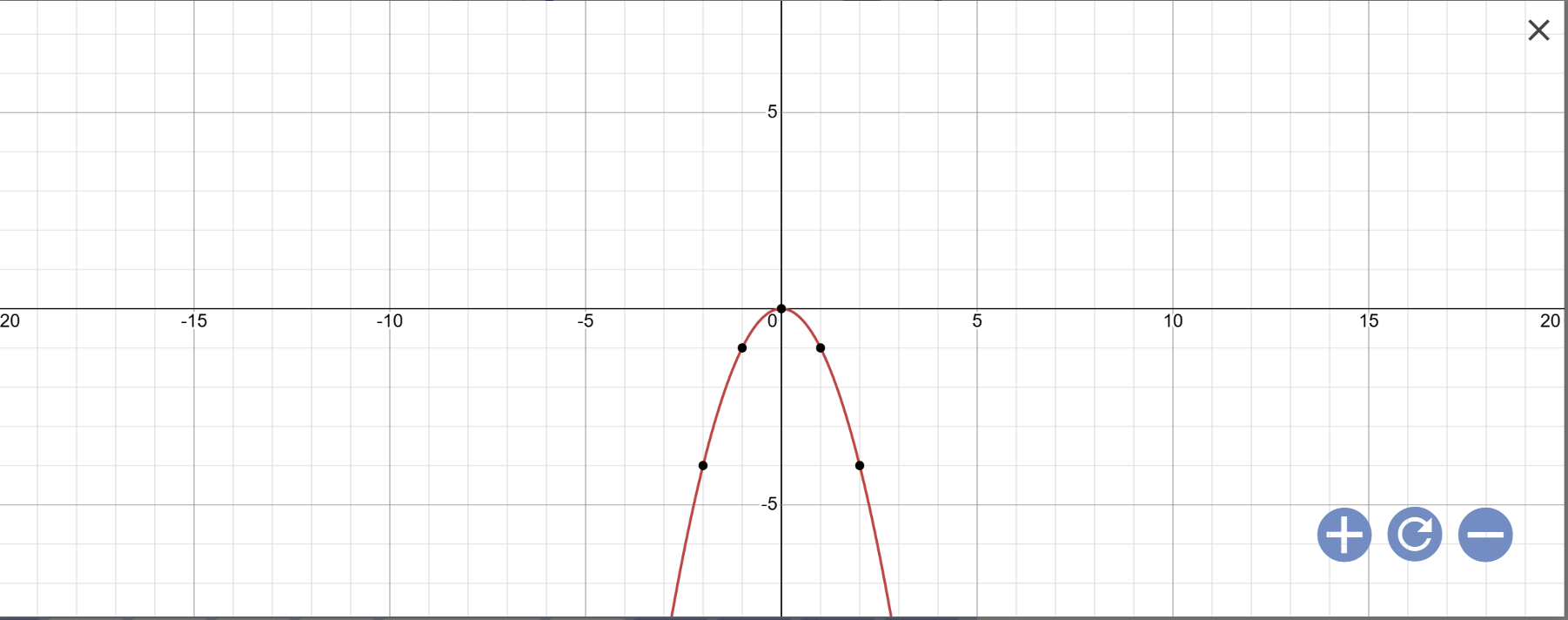
b: Thay y=-3 vào \(y=-x^2\), ta được:
\(-x^2=-3\)
=>\(x^2=3\)
=>\(\left[{}\begin{matrix}x=\sqrt{3}\\x=-\sqrt{3}\end{matrix}\right.\)
Vậy: Các điểm cần tìm là \(A\left(\sqrt{3};-3\right);B\left(-\sqrt{3};-3\right)\)
c: Thay y=3 vào \(y=-x^2\), ta được:
\(-x^2=3\)
=>\(x^2=-3\)(vô lý)
Vậy: Không có điểm nào thỏa mãn yêu cầu
d: Thay y=2x vào \(y=-x^2\), ta được:
\(-x^2=2x\)
=>\(x^2+2x=0\)
=>x(x+2)=0
=>\(\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Khi x=0 thì \(y=2\cdot0=0\)
Khi x=-2 thì \(y=2x=2\cdot\left(-2\right)=-4\)
Vậy: Các điểm cần tìm là O(0;0); C(-2;-4)
e: Thay y=x vào y=-x^2, ta được:
\(x=-x^2\)
=>\(x^2+x=0\)
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=x=0\\y=x=-1\end{matrix}\right.\)
Vậy: Có 1 điểm khác gốc tọa độ mà thuộc đồ thị hàm số y=-x^2 nhưng cách đều hai trục tọa độ






