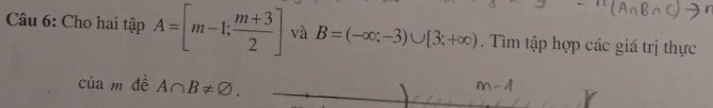Để A khác rỗng thì \(m-1< =\dfrac{m+3}{2}\)
=>\(2\left(m-1\right)< =m+3\)
=>\(2m-2< =m+3\)
=>\(m< =5\left(1\right)\)
\(B=\left(-\infty;-3\right)\cup[3;+\infty)\)
=>B=R\[-3;3)
Để A giao B bằng rỗng thì \(\left[m-1;\dfrac{m+3}{2}\right]\subset[-3;3)\)
=>\(\left\{{}\begin{matrix}m-1>=-3\\\dfrac{m+3}{2}< 3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>=-2\\m+3< =6\end{matrix}\right.\)
=>-2<=m<=3(2)
Từ (1),(2) suy ra để A giao B bằng rỗng thì -2<=m<=3
=>Để A giao B khác rỗng thì \(\left[{}\begin{matrix}m< -2\\\left\{{}\begin{matrix}m>3\\m< =5\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< -2\\3< m< =5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
