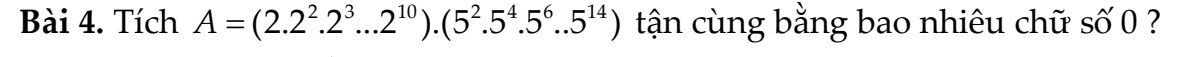Ta có:
\(A=\left(2\cdot2^2\cdot...\cdot2^{10}\right)\cdot\left(5^2\cdot5^4\cdot...\cdot5^{14}\right)\\ =2^{1+2+...+10}\cdot5^{2+4+...+14}\)
\(1+2+3+...+10=\dfrac{\left[\left(10-1\right):1+1\right]\cdot\left(10+1\right)}{2}=55\)
\(2+4+..+14=\dfrac{\left[\left(14-2\right):2+1\right]\cdot\left(14+2\right)}{2}=56\)
\(\Rightarrow A=2^{55}\cdot5^{56}=2^{55}\cdot5^{55}\cdot5\\ =\left(2\cdot5\right)^{55}\cdot5=10^{55}\cdot5\)
=> A có 55 chữ số 0 ở tận cùng
\(A=\left(2.2^2.2^3.....2^{10}\right).\left(5^2.5^4.5^6....5^{14}\right)\)
\(A=2^{1+2+3+...+10}.5^{2+4+6+...+14}\)
\(A=2^{55}.5^{56}\)
\(A=2^{55}.5.5^{55}\)
\(A=10^{55}.5^{55}\)
\(\Rightarrow\)A có \(55\) chữ số \(0\) ở tận cùng.
\(A=\left(2.2^2.2^3...2^{10}\right).\left(5^2.5^4.5^6...5^{14}\right)\)
\(A=\left(2^{1+2+...+10}\right).\left(5^{2+4+...+10}\right)\)
\(A=2^{55}.5^{55}=10^{55}=\overline{.....0}\)
Nên A có tận cùng 55 chữ số 0