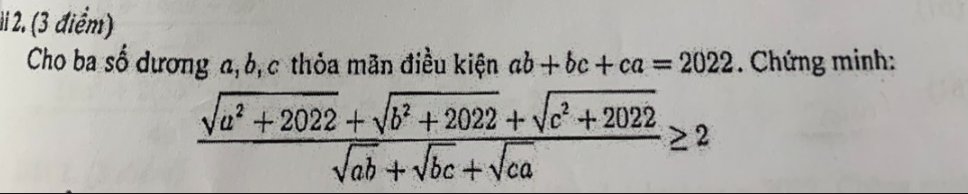Ta có : \(ab+bc+ca=2022\left(a;b;c>0\right)\)
\(\Rightarrow a^2+2022=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right)\left(a+c\right)\)
\(\Rightarrow\sqrt{a^2+2022}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{a+b+a+c}{2}=a+\dfrac{b+c}{2}\left(Bđt.Cauchy\right)\)
Tương tự ta chứng minh được
\(\sqrt{b^2+2022}\le b+\dfrac{c+a}{2}\)
\(\sqrt{c^2+2022}\le c+\dfrac{a+b}{2}\)
\(\Rightarrow\sqrt{a^2+2022}+\sqrt{b^2+2022}+\sqrt{c^2+2022}\le a+b+c+\dfrac{a+b+b+c+c+a}{2}=2\left(a+b+c\right)\left(1\right)\)
Áp dụng Bất đẳng thức Bunhiacopxki ta được :
\(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\le\sqrt{\left(a+b+c\right)^2}=a+b+c\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow\dfrac{\sqrt{a^2+2022}+\sqrt{b^2+2022}+\sqrt{c^2+2022}}{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}\ge\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=\sqrt{674}\)
Vậy \(đpcm\)
\(a^2+2022=a^2+ab+bc+ca=\left(a+b\right)\left(c+a\right)\ge\left(\sqrt{ab}+\sqrt{ac}\right)^2\)
\(\Rightarrow\sqrt{a^2+2022}\ge\sqrt{ab}+\sqrt{ac}\)
Tương tự:
\(\sqrt{b^2+2022}\ge\sqrt{ab}+\sqrt{bc}\)
\(\sqrt{c^2+2022}\ge\sqrt{ac}+\sqrt{bc}\)
\(\Rightarrow\dfrac{\sqrt{a^2+2022}+\sqrt{b^2+2022}+\sqrt{c^2+2022}}{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}\ge\dfrac{\sqrt{ab}+\sqrt{ac}+\sqrt{ab}+\sqrt{bc}+\sqrt{ac}+\sqrt{bc}}{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}=2\)
Dấu "=" xảy ra khi \(a=b=c=\sqrt{\dfrac{2022}{3}}=\sqrt{674}\)