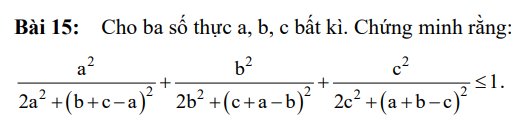\(\Leftrightarrow\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}+\dfrac{2b^2}{2b^2+\left(c+a-b\right)^2}+\dfrac{2c^2}{2c^2+\left(a+b-c\right)^2}\le2\)
\(\Leftrightarrow\dfrac{2a^2}{2a^2+\left(b+c-a\right)^2}-1+\dfrac{2b^2}{2b^2+\left(c+a-b\right)^2}-1+\dfrac{2c^2}{2c^2+\left(a+b-c\right)}-1\le2-3\)
\(\Leftrightarrow\dfrac{\left(b+c-a\right)^2}{2a^2+\left(b+c-a\right)^2}+\dfrac{\left(c+a-b\right)^2}{2b^2+\left(c+a-b\right)^2}+\dfrac{\left(a+b-c\right)^2}{2c^2+\left(a+b-c\right)^2}\ge1\)
Đặt \(\left\{{}\begin{matrix}b+c-a=x\\c+a-b=y\\a+b-c=z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{y+z}{2}\\b=\dfrac{z+x}{2}\\c=\dfrac{x+y}{2}\end{matrix}\right.\)
BĐT cần chứng minh trở thành:
\(\dfrac{x^2}{2\left(\dfrac{y+z}{2}\right)^2+x^2}+\dfrac{y^2}{2\left(\dfrac{z+x}{2}\right)^2+y^2}+\dfrac{z^2}{2\left(\dfrac{x+y}{2}\right)^2+z^2}\ge1\)
\(\Leftrightarrow\dfrac{2x^2}{\left(y+z\right)^2+2x^2}+\dfrac{2y^2}{\left(z+x\right)^2+2y^2}+\dfrac{2z^2}{\left(x+y\right)^2+2z^2}\ge1\)
Thật vậy, ta có:
\(\left(y+z\right)^2\le2\left(y^2+z^2\right)\Rightarrow\dfrac{2x^2}{\left(y+z\right)^2+2x^2}\ge\dfrac{2x^2}{2\left(y+z\right)^2+2x^2}=\dfrac{x^2}{x^2+y^2+z^2}\)
Tương tự:
\(\dfrac{2y^2}{\left(z+x\right)^2+2y^2}\ge\dfrac{y^2}{x^2+y^2+z^2}\)
\(\dfrac{2z^2}{\left(x+y\right)^2+2z^2}\ge\dfrac{z^2}{x^2+y^2+z^2}\)
Cộng vế:
\(\dfrac{2x^2}{\left(y+z\right)^2+2x^2}+\dfrac{2y^2}{\left(z+x\right)^2+2y^2}+\dfrac{2z^2}{\left(x+y\right)^2+2z^2}\ge\dfrac{x^2+y^2+z^2}{x^2+y^2+z^2}=1\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z\) hay \(a=b=c\)